题目内容
(本题满分12分)设等比数列{ }的前
}的前 项和
项和 ,首项
,首项 ,公比
,公比 .
.
(Ⅰ)证明: ;
;
(Ⅱ)若数列{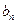 }满足
}满足 ,
, ,求数列{
,求数列{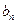 }的通项公式;
}的通项公式;
(Ⅲ)若 ,记
,记 ,数列{
,数列{ }的前项和为
}的前项和为 ,求证:当
,求证:当 时,
时, .
.
 }的前
}的前 项和
项和 ,首项
,首项 ,公比
,公比 .
.(Ⅰ)证明:
 ;
;(Ⅱ)若数列{
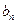 }满足
}满足 ,
, ,求数列{
,求数列{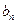 }的通项公式;
}的通项公式;(Ⅲ)若
 ,记
,记 ,数列{
,数列{ }的前项和为
}的前项和为 ,求证:当
,求证:当 时,
时, .
.解:(Ⅰ)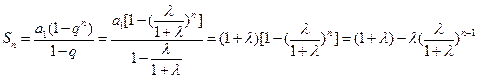
而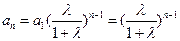 所以
所以 ………………………………3分
………………………………3分
(Ⅱ)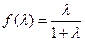 ,
,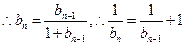 , ……………………5分
, ……………………5分
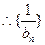 是首项为
是首项为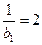 ,公差为1的等差数列,
,公差为1的等差数列,
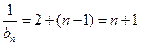 ,即
,即 . ………………7分
. ………………7分
(Ⅲ) 时,
时, 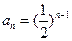 ,
, 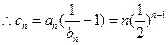 ………………8分
………………8分
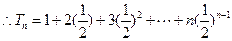
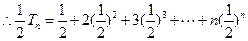
相减得
 , ………………10分
, ………………10分
又因为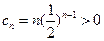 ,
,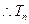 单调递增,
单调递增,
 故当
故当 时,
时,  . ………12分
. ………12分
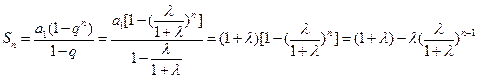
而
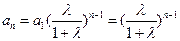 所以
所以 ………………………………3分
………………………………3分(Ⅱ)
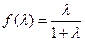 ,
,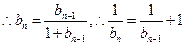 , ……………………5分
, ……………………5分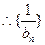 是首项为
是首项为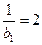 ,公差为1的等差数列,
,公差为1的等差数列, 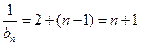 ,即
,即 . ………………7分
. ………………7分(Ⅲ)
 时,
时, 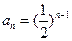 ,
, 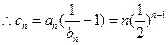 ………………8分
………………8分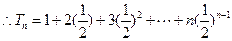
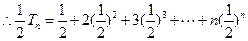
相减得

 , ………………10分
, ………………10分又因为
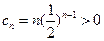 ,
,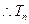 单调递增,
单调递增,  故当
故当 时,
时,  . ………12分
. ………12分略

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

 的通项公式;
的通项公式;  ,求数列
,求数列
 ,
,
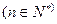 ,记
,记 ,设数列
,设数列 的前
的前 项和为
项和为 ,求证:对任意正整数
,求证:对任意正整数 ;
; 的值为 ( )
的值为 ( )


 满足
满足 则
则 的最小值为_________.
的最小值为_________. 的前
的前 项和
项和 ,利用倒序求和的方法得:
,利用倒序求和的方法得: ;类似的,记等比数列
;类似的,记等比数列 的前
的前 ,且
,且
 ,试类比等差数列求和的方法,可将
,试类比等差数列求和的方法,可将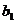 ,末项
,末项 与项数
与项数 _______________。
_______________。 满足
满足 ,且对任意的正整数
,且对任意的正整数 都有
都有 ,若数列
,若数列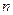 项和为
项和为 ,则
,则 的前n项和为
的前n项和为 ,且
,且 ,数列
,数列 为等差数列,且
为等差数列,且
 ,求数列
,求数列 的前n项和
的前n项和 。
。 是公差为-2的等差数列,如果
是公差为-2的等差数列,如果 ,那么
,那么 ( )
( )  B.
B. 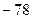 C
C 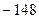 D.
D. 