题目内容
定义在R上的函数f(x)满足 ,且当0≤x1<x2≤1时,有f(x1)≤f(x2),则
,且当0≤x1<x2≤1时,有f(x1)≤f(x2),则 的值为
的值为
- A.
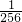
- B.
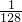
- C.

- D.

B
分析:根据已知条件,可求出f( )=
)= ,f(
,f( )=
)= ,再因为当0≤x1<x2≤1时,有f(x1)≤f(x2),可找到
,再因为当0≤x1<x2≤1时,有f(x1)≤f(x2),可找到 的范围为
的范围为 ,再根据f(
,再根据f( )=
)= ,f(
,f( )=
)= 求出
求出 的值,为同一个值,所以
的值,为同一个值,所以 的值也等于这个值.
的值也等于这个值.
解答:∵定义在R上的函数f(x)满足 ,
,
∴f(1)+f(0)=1,∴f(1)=1
f( )+f(1-
)+f(1- )=1,∴f(
)=1,∴f( )=
)=
f( )=
)= f(1),∴f(
f(1),∴f( )=
)=
f( )=
)=
∵ ,且当0≤x1<x2≤1时,有f(x1)≤f(x2),
,且当0≤x1<x2≤1时,有f(x1)≤f(x2),
∴ ,
,
又∵f( )=
)= f(
f( )=
)= f(
f( )=…=
)=…= f(
f( )=
)=
f( )=
)= f(
f( )=
)= f(
f(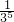 )=…=
)=…= f(1)=
f(1)=
∴ =
= =
=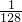
故选B
点评:本题主要考查了根据函数性质求函数值,注意赋值法的应用.
分析:根据已知条件,可求出f(
 )=
)= ,f(
,f( )=
)= ,再因为当0≤x1<x2≤1时,有f(x1)≤f(x2),可找到
,再因为当0≤x1<x2≤1时,有f(x1)≤f(x2),可找到 的范围为
的范围为 ,再根据f(
,再根据f( )=
)= ,f(
,f( )=
)= 求出
求出 的值,为同一个值,所以
的值,为同一个值,所以 的值也等于这个值.
的值也等于这个值.解答:∵定义在R上的函数f(x)满足
 ,
,∴f(1)+f(0)=1,∴f(1)=1
f(
 )+f(1-
)+f(1- )=1,∴f(
)=1,∴f( )=
)=
f(
 )=
)= f(1),∴f(
f(1),∴f( )=
)=
f(
 )=
)=
∵
 ,且当0≤x1<x2≤1时,有f(x1)≤f(x2),
,且当0≤x1<x2≤1时,有f(x1)≤f(x2),∴
 ,
,又∵f(
 )=
)= f(
f( )=
)= f(
f( )=…=
)=…= f(
f( )=
)=
f(
 )=
)= f(
f( )=
)= f(
f(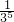 )=…=
)=…= f(1)=
f(1)=
∴
 =
= =
=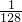
故选B
点评:本题主要考查了根据函数性质求函数值,注意赋值法的应用.

练习册系列答案
相关题目