题目内容
已知两条抛物线 y1=x2+2mx+4，y2=x2+mx-m 中至少有一条与x轴有公共点，则实数m的取值范围是________．
m≤-2 或m≥0
分析：由于两条抛物线 y1=x2+2mx+4，y2=x2+mx-m 中至少有一条与x轴有公共点的情况比较多，故考虑利用其反面情况：两条抛物线 y1=x2+2mx+4，y2=x2+mx-m 与x轴都没有公共点，可得则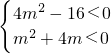
，解不等式组可得
解答：若两条抛物线 y1=x2+2mx+4，y2=x2+mx-m 与x轴都没有公共点
则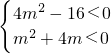
解不等式组可得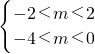
∴-2＜m＜0
从而可得两条抛物线 y1=x2+2mx+4，y2=x2+mx-m 中至少有一条与x轴有公共点即为上述的反面
∴m≥0或m≤-2
故答案为：m≤-2或m≥0
点评：本题主要考查了直线与抛物线的位置关系的应用，解题的关键是考虑利用补集单思想进行求解，要注意此方法的应用．
分析：由于两条抛物线 y1=x2+2mx+4，y2=x2+mx-m 中至少有一条与x轴有公共点的情况比较多，故考虑利用其反面情况：两条抛物线 y1=x2+2mx+4，y2=x2+mx-m 与x轴都没有公共点，可得则
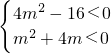，解不等式组可得解答：若两条抛物线 y1=x2+2mx+4，y2=x2+mx-m 与x轴都没有公共点
则
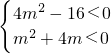
解不等式组可得
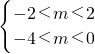
∴-2＜m＜0
从而可得两条抛物线 y1=x2+2mx+4，y2=x2+mx-m 中至少有一条与x轴有公共点即为上述的反面
∴m≥0或m≤-2
故答案为：m≤-2或m≥0
点评：本题主要考查了直线与抛物线的位置关系的应用，解题的关键是考虑利用补集单思想进行求解，要注意此方法的应用．
练习册系列答案
高效智能课时作业系列答案
相关题目
;
.