题目内容
已知函数f（x）的定义域为[0，1]，且同时满足：（Ⅰ）对任意x∈[0，1]，总有f（x）≥3；（Ⅱ）f（1）=4；（Ⅲ）若x1≥0，x2≥0，x1+x2≤1，则有f（x1+x2）≥f（x1）+f（x2）-3
（1）试求f（0）的值；
（2）试求函数f（x）的最大值；
（3）试证明：当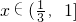
时，f（x）＜3x+3．
解：（1）令x1=x2=0可得，f（0）≥2f（0）-3
∴f（0）≤3
∵对任意x∈[0，1]，总有f（x）≥3
∴f（0）≥3
∴f（0）=3
（2）任取x1＜x2∈[0，1]
则f（x2）=f[x1+（x2-x1）]≥f（x1）+f（x2-x1）-3
由x2-x1＞0可得f（x2-x1）≥3
∴当x∈[0，1]时，f（x）≤f（1）=4
∴函数的最大值为4
（3）证明：当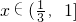时，f（x）≤f（1）=4=1+3
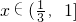时，3x+3＞3×
+3=4
∴f（x）＜3x+3
分析：（1）令x1=x2=0可得，f（0）≤3，结合已知可知f（0）≥3，从而可求f（0）
（2）任取x1＜x2∈[0，1]，则f（x2）=f[x1+（x2-x1）]≥f（x1）+f（x2-x1）-3，则可得f（x）≤f（1），从而可求函数的最大值
（3）由已知可证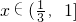，时，f（x）≤f（1）=4，3x+3＞4，可证
点评：本题主要考查了抽象函数利用赋值法求解函数的函数值，及利用构造法证明函数的单调性及由函数的单调性解不等式等知识的综合应用．
∴f（0）≤3
∵对任意x∈[0，1]，总有f（x）≥3
∴f（0）≥3
∴f（0）=3
（2）任取x1＜x2∈[0，1]
则f（x2）=f[x1+（x2-x1）]≥f（x1）+f（x2-x1）-3
由x2-x1＞0可得f（x2-x1）≥3
∴当x∈[0，1]时，f（x）≤f（1）=4
∴函数的最大值为4
（3）证明：当
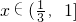时，f（x）≤f（1）=4=1+3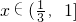时，3x+3＞3×+3=4∴f（x）＜3x+3
分析：（1）令x1=x2=0可得，f（0）≤3，结合已知可知f（0）≥3，从而可求f（0）
（2）任取x1＜x2∈[0，1]，则f（x2）=f[x1+（x2-x1）]≥f（x1）+f（x2-x1）-3，则可得f（x）≤f（1），从而可求函数的最大值
（3）由已知可证，
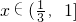时，f（x）≤f（1）=4，3x+3＞4，可证点评：本题主要考查了抽象函数利用赋值法求解函数的函数值，及利用构造法证明函数的单调性及由函数的单调性解不等式等知识的综合应用．
练习册系列答案
相关题目
