题目内容
已知数列{an}的各项均为正数，它的前n项和Sn满足
，并且a2，a4，a9成等比数列．
（1）求数列{an}的通项公式；
（2）设
，Tn是数列{bn}的前n项和，求证：
．
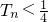解：（1）当n=1时，
，∴a1=1或a1=2
当n≥2时，
①
∵
∴①-②，并整理得（an+an-1）（an-an-1-3）=0
∵数列{an}的各项均为正数
∴an-an-1=3
当a1=1时，an=3n-2，此时满足a2，a4，a9成等比数列．
当a1=2时，an=3n-1，此时不满足a2，a4，a9成等比数列
∴an=3n-2
（2）根据（1）的结论可得
∴
=
∴
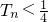
分析：（1）先利用条件，求出数列的首项，再利用当n≥2时，，可求数列的通项，利用a2，a4，a9成等比数列，求出满足条件的数列的通项．
（2）利用（1）的结论，先进行放缩，再利用裂项法可求数列{bn}的前n项和，从而得证．
点评：本题以数列的前n项和为载体，考查数列通项的求解，考查放缩法，考查裂项法求和，解题的关键是适度放缩，再利用裂项法．
，∴a1=1或a1=2当n≥2时，
①∵
∴①-②，并整理得（an+an-1）（an-an-1-3）=0
∵数列{an}的各项均为正数
∴an-an-1=3
当a1=1时，an=3n-2，此时满足a2，a4，a9成等比数列．
当a1=2时，an=3n-1，此时不满足a2，a4，a9成等比数列
∴an=3n-2
（2）根据（1）的结论可得
∴
=∴
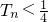
分析：（1）先利用条件
，求出数列的首项，再利用当n≥2时，，可求数列的通项，利用a2，a4，a9成等比数列，求出满足条件的数列的通项．（2）利用（1）的结论，先进行放缩，再利用裂项法可求数列{bn}的前n项和，从而得证．
点评：本题以数列的前n项和为载体，考查数列通项的求解，考查放缩法，考查裂项法求和，解题的关键是适度放缩，再利用裂项法．
练习册系列答案
相关题目
，则下列各数是否为数列中的项？如果是，是第几项？如果不是，为什么？（1）
（2）
，则下列各数是否为数列中的项？如果是，是第几项？如果不是，为什么？（1）
（2）