题目内容
已知A、B分别为直二面角αlβ的面α、β内的点,AB与α、β所成的角分别为45°、30°,又AC⊥l于C,BD⊥l于D,求二面角CABD的大小.
解:![]() AC⊥平面β
AC⊥平面β![]() ∠ABC=30°.
∠ABC=30°.
同理,∠BAD=45°.
设AC=1,则BC=![]() ,BD=AD=
,BD=AD=![]() ,CD=1.
,CD=1.
设![]() 、
、![]() 、
、![]() 的单位向量分别为a、b、c,在△BCD中,
的单位向量分别为a、b、c,在△BCD中,
CB=![]() ,CD=1,故cos∠BCD=
,CD=1,故cos∠BCD=![]() ,
,
∴a·b=![]() ,b·c=0,c·a=0.
,b·c=0,c·a=0.
过C、D分别作AB的垂线,垂足分别为E、F,且F是AB的中点,
![]() =
=![]() (
(![]() +
+![]() )=
)=![]() (c-b+
(c-b+![]() a-b)=
a-b)=![]() (
(![]() a-2b+c),
a-2b+c),
由于A、E、B三点共线,∴可设![]() =x
=x![]() +(1-x)
+(1-x) ![]() =x·3a+(1-x)·c.
=x·3a+(1-x)·c.
又![]() =
=![]() -
-![]() =
=![]() a-c且
a-c且![]() ⊥
⊥![]() ,
,
∴![]() ·
·![]() =[
=[![]() xa+(1-x)c]·(
xa+(1-x)c]·(![]() a-c)=4x-1=0.∴x=
a-c)=4x-1=0.∴x=![]() .
.
故![]() =
=![]() (a+
(a+![]() c),
c),
![]() ·
·![]() =
=![]() ·
·![]() =
=![]() (
(![]() a-2b-c)·(a+
a-2b-c)·(a+![]() c)=
c)=![]() ,
,
又![]() 2=
2=![]() (a+
(a+![]() c)2=
c)2=![]() ,
,
∴|![]() |=
|=![]() .
.
同理,| ![]() |=1.
|=1.
∴cos〈![]() ,
,![]() 〉=
〉=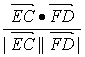 =
=![]() =
=![]() .
.
∴二面角CABD的大小为arccos![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,  ,
, ,
,
 是
是 和
和 的交点, 若
的交点, 若 .
.  的长; (2)求点
的长; (2)求点 到平面
到平面 的距离;
的距离;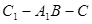 的平面角的正弦值的大小.
的平面角的正弦值的大小.
 A
A AC=3
AC=3 BC
BC ,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
 C
C sin
sin , -
, - ) ……………………… 3分
) ……………………… 3分 =(2, -
=(2, - =(0,
-3, -h) ……… 4分
=(0,
-3, -h) ……… 4分 =(a, b, c),则可求得
=(a, b, c),则可求得 |=
|= =(x, y, z),则可求得
=(x, y, z),则可求得 满足cos
满足cos =
= ………
11分
………
11分