题目内容
设f(x)在[0,+∞)上连续,且| ∫ | x 0 |
| π |
| 2 |
分析:根据题意,先设出被积函数的原函数,再直接计算在区间(0,x)上的定积分即可求得被积函数的原函数,再求导即得f(x)=1+cosx-xsinx,从而求得f(
).
| π |
| 2 |
解答:解:设f(x)的原函数是F(x),
则由∫x0f(t)dt=x(1+cosx)得:
F(x)-F(0)=x(1+cosx),
∴F′(x)-F′(0)=1+cosx-xsinx,
即f(x)=1+cosx-xsinx,
∴f(
)=1+cos
-
sin
=1-
,
故答案为:1-
.
则由∫x0f(t)dt=x(1+cosx)得:
F(x)-F(0)=x(1+cosx),
∴F′(x)-F′(0)=1+cosx-xsinx,
即f(x)=1+cosx-xsinx,
∴f(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故答案为:1-
| π |
| 2 |
点评:本题考查定积分的简单应用,关键是找出被积函数的原函数,本题属于基础题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
设f(x)在[0,1]上有定义,要使函数f(x-a)+f(x+a)有定义,则a的取值范围为( )
A、(-∞,-
| ||||
B、[-
| ||||
C、(
| ||||
D、(-∞,-
|
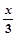 )=
)=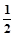 f(x);(3)f(1-x)=1-f(x),则f(
f(x);(3)f(1-x)=1-f(x),则f(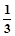 )+f(
)+f(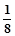 )=( )
)=( )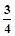 B.
B.