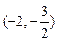题目内容
设函数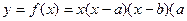 、
、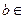 R)。
R)。
(1)若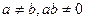 ,过两点(0,0)、(
,过两点(0,0)、(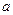 ,0)的中点作与
,0)的中点作与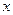 轴垂直的直线,与函数
轴垂直的直线,与函数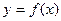 的图象交于点
的图象交于点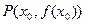 ,求证:函数
,求证:函数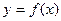 在点P处的切线点为(
在点P处的切线点为(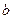 ,0)。
,0)。
(2)若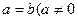 ),且当
),且当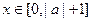 时
时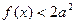 恒成立,求实数
恒成立,求实数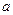 的取值范围。
的取值范围。
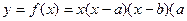 、
、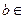 R)。
R)。(1)若
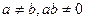 ,过两点(0,0)、(
,过两点(0,0)、(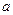 ,0)的中点作与
,0)的中点作与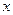 轴垂直的直线,与函数
轴垂直的直线,与函数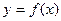 的图象交于点
的图象交于点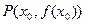 ,求证:函数
,求证:函数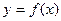 在点P处的切线点为(
在点P处的切线点为(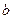 ,0)。
,0)。(2)若
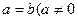 ),且当
),且当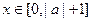 时
时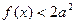 恒成立,求实数
恒成立,求实数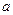 的取值范围。
的取值范围。 (1)同解析 (2)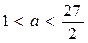
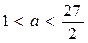
1)由已知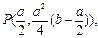
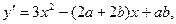
所求,所求切线斜率为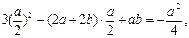
切线方程为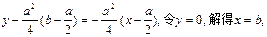
所以,函数y=f (x)过点P的切线过点(b,0)
(2)因为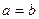 ,所以
,所以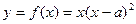 ,
,
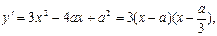
当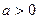 时,函数
时,函数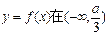 上单调递增,在(
上单调递增,在(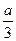 ,
,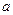 )单调递减,
)单调递减,
在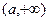 上单调递增.
上单调递增.
所以,根据题意有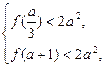 即
即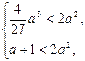
解之得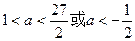 ,结合
,结合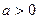 ,所以
,所以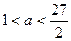
当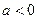 时,函数
时,函数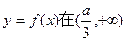 单调递增。
单调递增。
所以,根据题意有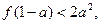
即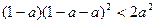 , 整理得
, 整理得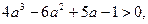 (
(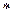 )
)
令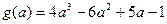 ,
,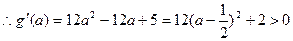
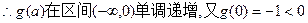 ,所以“
,所以“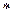 ”不等式无解。
”不等式无解。
综上可知: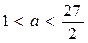 。
。
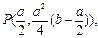
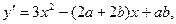
所求,所求切线斜率为
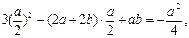
切线方程为
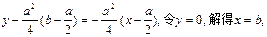
所以,函数y=f (x)过点P的切线过点(b,0)
(2)因为
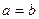 ,所以
,所以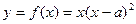 ,
,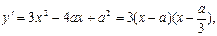
当
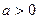 时,函数
时,函数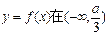 上单调递增,在(
上单调递增,在(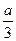 ,
,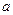 )单调递减,
)单调递减,在
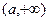 上单调递增.
上单调递增. 所以,根据题意有
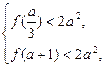 即
即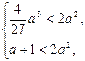
解之得
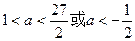 ,结合
,结合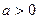 ,所以
,所以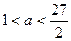
当
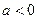 时,函数
时,函数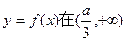 单调递增。
单调递增。 所以,根据题意有
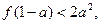
即
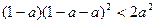 , 整理得
, 整理得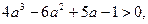 (
(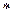 )
)令
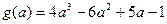 ,
,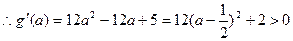
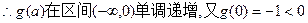 ,所以“
,所以“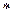 ”不等式无解。
”不等式无解。 综上可知:
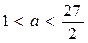 。
。 
练习册系列答案
相关题目
 的图像如图所示,则
的图像如图所示,则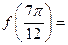 。
。
 ;(2)
;(2) ;(3)
;(3) ;
; ;(5)
;(5) ,
,


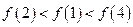



 在
在 处连续,试确定a的值
处连续,试确定a的值 ,在区间
,在区间 上画出函数
上画出函数 的图像。
的图像。
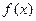 的图象是如图所示的折线段OAB,点A坐标为
的图象是如图所示的折线段OAB,点A坐标为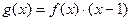 ,
,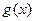 最大值为 。
最大值为 。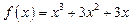 的图象按向量
的图象按向量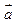 平移后得到函数
平移后得到函数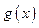 的图象,若函数
的图象,若函数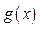 满足
满足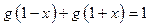 ,则向量
,则向量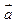 的坐标是( )
的坐标是( )