题目内容
(2012•青岛一模)星空电视台组织篮球技能大赛,每名选手都要进行运球、传球、投篮三项比赛,每个选手在各项比赛中获得合格与不合格的机会相等,且互不影响.现有A、B、C、D、E、F六位选手参加比赛,电视台根据比赛成绩对前2名进行表彰奖励.
(Ⅰ)求A至少获得一个合格的概率;
(Ⅱ)求A与B只有一个受到表彰奖励的概率.
(Ⅰ)求A至少获得一个合格的概率;
(Ⅱ)求A与B只有一个受到表彰奖励的概率.
分析:(Ⅰ)根据题意将投篮合格、不合格分别编号,再列出所有的基本事件,再由古典概型公式,计算可得答案;
(Ⅱ)根据题意将所有受到表彰奖励可能的结果一一列出,再由古典概型公式,计算可得答案.
(Ⅱ)根据题意将所有受到表彰奖励可能的结果一一列出,再由古典概型公式,计算可得答案.
解答:解:(Ⅰ)记A运球,传球,投篮合格分别记为W1,W2,W3,不合格为
1,
2,
则A参赛的所有可能的结果为(W1,W2,W3),(
1,W2,W3),(W1,
,W3),(W1,W2,
),
(
,
,W3),(
,W2,
),(W1,
,
),(
,
,
)共8种,
由上可知A至少获得一个合格对应的可能结果为7种,
∴A至少获得一个合格的概率为:P=
(Ⅱ)所有受到表彰奖励可能的结果为{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},
{C,D},{C,E},{C,F},{D,E},{D,F},{E,F}共15个,
则A与B只有一个受到表彰奖励的结果为{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F}共8种
则A与B只有一个受到表彰奖励的概率为P=
. |
| W |
. |
| W |
. |
| W3 |
则A参赛的所有可能的结果为(W1,W2,W3),(
. |
| W |
. |
| W2 |
. |
| W3 |
(
. |
| W1 |
. |
| W2 |
. |
| W1 |
. |
| W3 |
. |
| W2 |
. |
| W3 |
. |
| W1 |
. |
| W2 |
. |
| W3 |
由上可知A至少获得一个合格对应的可能结果为7种,
∴A至少获得一个合格的概率为:P=
| 7 |
| 8 |
(Ⅱ)所有受到表彰奖励可能的结果为{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},
{C,D},{C,E},{C,F},{D,E},{D,F},{E,F}共15个,
则A与B只有一个受到表彰奖励的结果为{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F}共8种
则A与B只有一个受到表彰奖励的概率为P=
| 8 |
| 15 |
点评:本题考查古典概型的计算,涉及列举法的应用,解题的关键是正确列举,分析得到事件的情况数目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
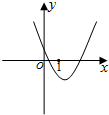 (2012•青岛一模)已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数g(x)=loga(x+b)的图象可能为
(2012•青岛一模)已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数g(x)=loga(x+b)的图象可能为