题目内容
设函数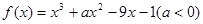 ,且曲线
,且曲线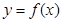 斜率最小的切线与直线
斜率最小的切线与直线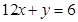 平行.求:(1)
平行.求:(1)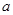 的值;(2)函数
的值;(2)函数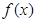 的单调区间.
的单调区间.
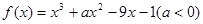 ,且曲线
,且曲线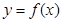 斜率最小的切线与直线
斜率最小的切线与直线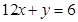 平行.求:(1)
平行.求:(1)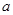 的值;(2)函数
的值;(2)函数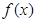 的单调区间.
的单调区间.(1) (2)增区间是
(2)增区间是 和
和 ,减区间是(-1,3)
,减区间是(-1,3)
 (2)增区间是
(2)增区间是 和
和 ,减区间是(-1,3)
,减区间是(-1,3)试题分析:(1)
 的定义域为R
的定义域为R
所以
 ,
,由条件得
 ,解得
,解得 或
或 (舍)
(舍)所以

(2)因为
 ,所以
,所以 ,
, ,解得
,解得 或
或
所以当
 或
或 时,
时,
当
 时,
时, ,
,所以
 的单调增区间是
的单调增区间是 和
和 ,减区间是(-1,3).
,减区间是(-1,3).点评:利用导数的几何意义可求出函数在某一点出的切线斜率,求增区间需解不等式
 ,求减区间需解不等式
,求减区间需解不等式

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
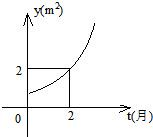
 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,则不等式组
,则不等式组 所确定的平面区域在
所确定的平面区域在 内的面积为 ( )
内的面积为 ( )



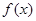 的定义域为R,最小正周期
的定义域为R,最小正周期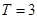 ,若
,若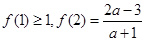 ,则
,则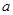 的取值范围是
的取值范围是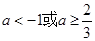
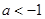
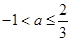
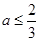
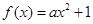 (
( ),
), .
. 与
与 处具有公共切线,求
处具有公共切线,求 的值;
的值; 时,求函数
时,求函数 在区间
在区间 上的最大值.
上的最大值.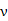 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度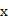 (单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当
(单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当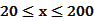 时,车流速度
时,车流速度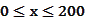 时,求函数
时,求函数 的表达式;
的表达式;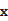 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)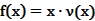 可以达到最大?并求出最大值。(精确到1辆/小时)
可以达到最大?并求出最大值。(精确到1辆/小时) = ;
= ;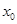 函数
函数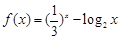 的零点,若
的零点,若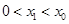 ,则
,则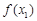 的值为( )
的值为( )