题目内容
设抛物线y2=2px(p>0)的焦点为F,Q是抛物线上除顶点外的任意一点,直线QO交准线于P点,过Q且平行于抛物线对称轴的直线交准线于R点,求证: •
•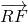 =0.
=0.
证明:设Q( ,y0),则R(-
,y0),则R(- ,y0),
,y0),
直线OQ的方程为y= x,
x,
将x=- 代入上式,得y=-
代入上式,得y=- ,
,
∴P(- ,-
,- ).又F(
).又F( ,0),
,0),
∴ =(p,
=(p, ),
),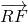 =(p,-y0).
=(p,-y0).
∴ •
•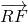 =0.
=0.
分析:先根据抛物线方程设出点Q和R,则直线OQ的方程可得,将x=- 代入即可得交点P的坐标,同时根据抛物线方程可知点F的坐标,进而表示出
代入即可得交点P的坐标,同时根据抛物线方程可知点F的坐标,进而表示出 和
和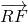 ,求得
,求得 •
•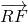 =0.
=0.
点评:本题主要考查了抛物线的应用,向量的计算.考查了学生综合把握抛物线基础知识的能力.
 ,y0),则R(-
,y0),则R(- ,y0),
,y0),直线OQ的方程为y=
 x,
x,将x=-
 代入上式,得y=-
代入上式,得y=- ,
,∴P(-
 ,-
,- ).又F(
).又F( ,0),
,0),∴
 =(p,
=(p, ),
),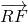 =(p,-y0).
=(p,-y0).∴
 •
•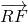 =0.
=0.分析:先根据抛物线方程设出点Q和R,则直线OQ的方程可得,将x=-
 代入即可得交点P的坐标,同时根据抛物线方程可知点F的坐标,进而表示出
代入即可得交点P的坐标,同时根据抛物线方程可知点F的坐标,进而表示出 和
和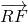 ,求得
,求得 •
•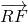 =0.
=0.点评:本题主要考查了抛物线的应用,向量的计算.考查了学生综合把握抛物线基础知识的能力.

练习册系列答案
相关题目
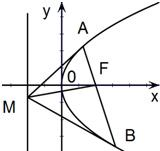 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)
设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,且A,B两点坐标分别为(x1,y1)、(x2,y2),y1>0,y2<0,M是抛物线的准线上的一点,O是坐标原点.若直线MA,MF,MB的斜率分别记为:KMA=a,KMF=b,KMB=c,(如图)