Question

设函数f(x)=x²-lnx²,

(1)若x∈［,e］时，不等式f(x)＞m的解集不是空集，求实数m的取值范围（e≈2.718 281 8…）

(2)若关于方程f(x)=x²+x-2a在区间（1，3）上有解，求实数a的取值范围.

Answer 1

解：(1)f′(x)=2x-=2，                                                               ?

当x∈［,1］时，f(x)＜0;当x∈(1,e)时，f′(x)＞0.?

所以f(x)在［,1］上单调递减，在（1，E）上单调递增，而f()=+2,f(e)=e²-2＞2e-2＞e, +2＜e,                                                                                                          

即f(x)的值域为［1，e²-2］.?

要使f(x)＞m的解集不是空集，则m∈(-∞,e²-2).                                                    ?

(2)方程x²+x-2a=x²-lnx²2lnx=2a-xlnx=a-在（1，3）上有解.?

设函数y₁=lnx,y₂=a-，即两函数的图象在区间（1，3）上有交点.?

所以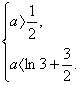故a的取值范围为（,+ln3）.