题目内容
已知数列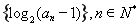 为等差数列,且
为等差数列,且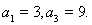
(1)求数列 的通项公式;
的通项公式;
(2)证明:
【答案】
(1)  (2)参考解析
(2)参考解析
【解析】
试题分析:(1)因为数列 为等差数列,又因为
为等差数列,又因为 所以通过这两项求出首项与公差.从而求出数列
所以通过这两项求出首项与公差.从而求出数列 的通项公式,即可求出数列
的通项公式,即可求出数列 的通项公式,本小题的关键是对一个较复杂的数列的理解.
的通项公式,本小题的关键是对一个较复杂的数列的理解.
(2)因为由(1)的到数列 的通项公式,根据题意需要求数列
的通项公式,根据题意需要求数列 前n项和公式,所以通过计算可求出通项公式,再利用等比数列的求和公式,即可得到结论.
前n项和公式,所以通过计算可求出通项公式,再利用等比数列的求和公式,即可得到结论.
试题解析:(I)解:设等差数列 的公差为
的公差为 .
.
由 即
即 =1.
=1.
所以 即
即
(II)证明: 
 ,
,


∴
考点:1.对数的运算.2.等差数列的性质.3.等比数列的性质.4.构造转化的思想.

练习册系列答案
相关题目
 为等差数列,且
为等差数列,且 ,
, .
. 的通项公式;
的通项公式;  ,
, 恒成立的实数m是否存在最小值?如果存在,求出m的最小值;如果不存在,说明理由.
恒成立的实数m是否存在最小值?如果存在,求出m的最小值;如果不存在,说明理由. 为等差数列,若
为等差数列,若 且它们的前
且它们的前 项和
项和 有最大值,则使得
有最大值,则使得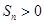 的
的 为等差数列,若
为等差数列,若 ,且它们的前
,且它们的前 项和
项和 有最大值,则使得
有最大值,则使得 的
的 为等差数列,
为等差数列,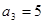 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,且有
,且有
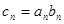 ,
, 的前
的前 ,求
,求