题目内容
已知f(x)=lg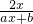 ,f(1)=0,当x>0时,恒有f(x)-f(
,f(1)=0,当x>0时,恒有f(x)-f( )=lgx.
)=lgx.
(1)求f(x)的解析式;
(2)若方程f(x)=lg(m+x)的解集是∅,求实数m的取值范围.
解:(1)∵当x>0时,恒有f(x)-f( )=lgx,∴lg
)=lgx,∴lg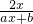 -lg
-lg 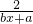 =lgx,∴(a-b)x2-(a-b)x=0.
=lgx,∴(a-b)x2-(a-b)x=0.
∵x≠0,∴a-b=0,即 a=b.
再由f(1)=0 可得a+b=2,∴a=b=1,
∴f(x)=lg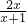 .
.
(2)由方程 lg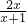 =lg(m+x)可得
=lg(m+x)可得 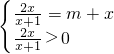 ,即
,即 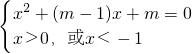 .
.
方程f(x)=lg(m+x)的解集是∅,故有两种情况:①方程x2+(m-1)x+m=0无解,
∴△<0,解得3-2 <m<3+2
<m<3+2 .
.
②方程x2+(m-1)x+m=0有解,且两根都在[-1,0]内,令g(x)=x2+(m-1)x+m,
则有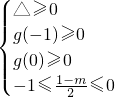 即
即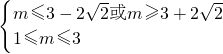 ,无解.
,无解.
综合①、②,实数m的取值范围是(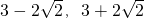 ).
).
分析:(1)根据 当x>0时,恒有f(x)-f( )=lgx,可得(a-b)x2-(a-b)x=0,求得 a=b,再由f(1)=0 可得a+b=2,从而求得a,b的值,可得函数的解析式.
)=lgx,可得(a-b)x2-(a-b)x=0,求得 a=b,再由f(1)=0 可得a+b=2,从而求得a,b的值,可得函数的解析式.
(2)由方程 lg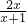 =lg(m+x)可得
=lg(m+x)可得 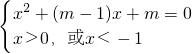 .由方程f(x)=lg(m+x)的解集是∅,可得:①方程x2+(m-1)x+m=0无解,即△<0,
.由方程f(x)=lg(m+x)的解集是∅,可得:①方程x2+(m-1)x+m=0无解,即△<0,
或②方程x2+(m-1)x+m=0有解,且两根都在[-1,0]内.分别求得实数m的取值范围,再取并集,即得所求.
点评:本题主要考查对数型函数的图象和性质的应用,体现了分类讨论和等价转化的数学思想,属于中档题.
 )=lgx,∴lg
)=lgx,∴lg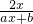 -lg
-lg 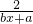 =lgx,∴(a-b)x2-(a-b)x=0.
=lgx,∴(a-b)x2-(a-b)x=0.∵x≠0,∴a-b=0,即 a=b.
再由f(1)=0 可得a+b=2,∴a=b=1,
∴f(x)=lg
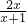 .
.(2)由方程 lg
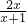 =lg(m+x)可得
=lg(m+x)可得 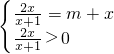 ,即
,即 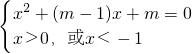 .
.方程f(x)=lg(m+x)的解集是∅,故有两种情况:①方程x2+(m-1)x+m=0无解,
∴△<0,解得3-2
 <m<3+2
<m<3+2 .
.②方程x2+(m-1)x+m=0有解,且两根都在[-1,0]内,令g(x)=x2+(m-1)x+m,
则有
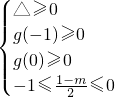 即
即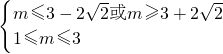 ,无解.
,无解.综合①、②,实数m的取值范围是(
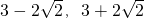 ).
).分析:(1)根据 当x>0时,恒有f(x)-f(
 )=lgx,可得(a-b)x2-(a-b)x=0,求得 a=b,再由f(1)=0 可得a+b=2,从而求得a,b的值,可得函数的解析式.
)=lgx,可得(a-b)x2-(a-b)x=0,求得 a=b,再由f(1)=0 可得a+b=2,从而求得a,b的值,可得函数的解析式.(2)由方程 lg
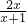 =lg(m+x)可得
=lg(m+x)可得 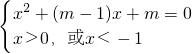 .由方程f(x)=lg(m+x)的解集是∅,可得:①方程x2+(m-1)x+m=0无解,即△<0,
.由方程f(x)=lg(m+x)的解集是∅,可得:①方程x2+(m-1)x+m=0无解,即△<0,或②方程x2+(m-1)x+m=0有解,且两根都在[-1,0]内.分别求得实数m的取值范围,再取并集,即得所求.
点评:本题主要考查对数型函数的图象和性质的应用,体现了分类讨论和等价转化的数学思想,属于中档题.

练习册系列答案
相关题目