题目内容
(2011•潍坊二模)已知数列{an}是各项均为为0的等差数列,Sn为其前n项和,且满足S2n-1=
,n∈N*.数列{bn}满足bn=
,Tn为数列{bn}的前n项和.
(I)求an,bn;
(Ⅱ)试比较T2n与2n2+
的大小.
| 1 |
| 2 |
| a | 2 n |
|
(I)求an,bn;
(Ⅱ)试比较T2n与2n2+
| n |
| 3 |
分析:(I)设数列{an}的首项为a1,公差为d,解关于a1与d的方程组,可求得a1=2,d=4,从而可求an,继而可求bn;
(Ⅱ)通过分组求和的方法可求得T2n,然后将T2n与2n2+
作差,T2n-(2n2+
)=
(4n-4n-1),验证n=1,2,3,时的符号,从而作出猜想,再用数学归纳法证明即可.
(Ⅱ)通过分组求和的方法可求得T2n,然后将T2n与2n2+
| n |
| 3 |
| n |
| 3 |
| 1 |
| 3 |
解答:解:(I)设数列{an}的首项为a1,公差为d,
在S2n-1=
an2中,令n=1,2,得
即
…2分
解得a1=2,d=4,d=-2(舍去),
∴an=4n-2…4分
∴bn=
…5分
(Ⅱ)T2n=1+2×2-3+22+2×4-3+24+…+22n-2+2×2n-3…9分
=1+22+24+…+22n-2+4(1+2+…+n)-3n
=
+4•
-3n
=
-
+2n2-n…8分
∴T2n-(2n2+
)=
(4n-4n-1),
当n=1时,
(4n-4n-1)=-
<0;
当n=2时,
(4n-4n-1)=
>0;
当n=3时,
(4n-4n-1)=
>0;
…
猜想当n≥2时,T2n>2n2+
,即n≥2时,4n>4n+1.
下面用数学归纳法证明:
①当n=2时,42=16,4×2+1=9,16>9,成立;
②假设当n=k(k≥2)时成立,即4k>4k+1.
则当n=k+1时,4k+1=4•4k>4(4k+1)=16k+4>4k+5=4(k+1)+1,
∴n=k+1时成立.
由①②得,当n≥2时,4n>4n+1成立…11分
综上,当n=1时,T2n<2n2+
,
当n≥2时,T2n>2n2+
…12分
在S2n-1=
| 1 |
| 2 |
|
|
解得a1=2,d=4,d=-2(舍去),
∴an=4n-2…4分
∴bn=
|
(Ⅱ)T2n=1+2×2-3+22+2×4-3+24+…+22n-2+2×2n-3…9分
=1+22+24+…+22n-2+4(1+2+…+n)-3n
=
| 1-4n |
| 1-4 |
| n(n+1) |
| 2 |
=
| 4n |
| 3 |
| 1 |
| 3 |
∴T2n-(2n2+
| n |
| 3 |
| 1 |
| 3 |
当n=1时,
| 1 |
| 3 |
| 1 |
| 3 |
当n=2时,
| 1 |
| 3 |
| 7 |
| 3 |
当n=3时,
| 1 |
| 3 |
| 51 |
| 3 |
…
猜想当n≥2时,T2n>2n2+
| n |
| 3 |
下面用数学归纳法证明:
①当n=2时,42=16,4×2+1=9,16>9,成立;
②假设当n=k(k≥2)时成立,即4k>4k+1.
则当n=k+1时,4k+1=4•4k>4(4k+1)=16k+4>4k+5=4(k+1)+1,
∴n=k+1时成立.
由①②得,当n≥2时,4n>4n+1成立…11分
综上,当n=1时,T2n<2n2+
| n |
| 3 |
当n≥2时,T2n>2n2+
| n |
| 3 |
点评:本题考查数列递推式,考查数学归纳法的应用,考查化归思想、分类讨论思想、方程思想的综合应用,属于难题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
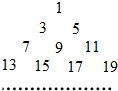 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 (2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足
(2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足