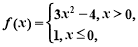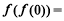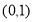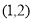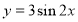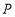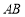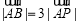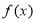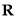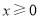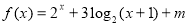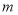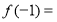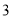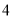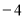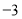题目内容
在平面直角坐标系中，已知点
．
（1）若
，且
，求角
的值；
（2）若
，求
的值．
（1）
,（2）
.
【解析】
试题分析：（1）由向量模的坐标表示，得
两边平方后就直接转化为同角三角函数关系，利用
得到
，再结合
的取值范围，解出，（2）由向量数量积的坐标表示，得
，同样利用同角三角函数关系：
解出
，另外对所求代数式
进行切化弦化简得
，两者结合可得结果.
试题解析：（1）由题意
∵
，∴
整理得， 4分
∵
，∴． 6分
（2）∵
，∴，
整理得
， 8分
∴
，∴． 10分
∴
=
==． 12分
考点：向量数量积，向量的模，同角三角函数关系.
练习册系列答案
一课一练课时达标系列答案
相关题目
