题目内容
设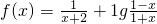
(Ⅰ)证明f(x)在(-1,1)上是减函数;
(Ⅱ)若f(x)的反函数为f-1(x),试证明方程f-1(x)=0只有唯一解;
(Ⅲ)解关于x的不等式: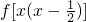 <
< .
.
证明:(I)f(x)在(-1,1)上递减
函数的定义域为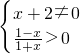 解得x∈(-1,1)
解得x∈(-1,1)
∵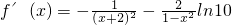 <0
<0
∴f(x)在(-1,1)上递减
(II)∵f(x)与f-1(x)的单调性相同
∴f-1(x)在定义域上递减
∵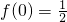
∴
∴f-1(x)=0有解,且唯一
(III)原不等式同解于
∵f(x)在(-1,1)上递减
∴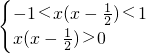 解得
解得
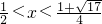 或
或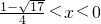
∴解集为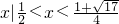 或
或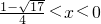 .
.
分析:(I)令分母不为0且真数大于0求出函数的定义域;利用导数的运算法则求出导函数,判断出导函数的符号,得证.
(II)根据互为反函数的单调性相同,得到f-1(x)递减;求出f(0)的值,得到反函数有根,据单调证得根唯一.
(III)将 用f(0)代替,利用f(x)的单调性去掉法则f,注意定义域;解二次不等式组求出解集.
用f(0)代替,利用f(x)的单调性去掉法则f,注意定义域;解二次不等式组求出解集.
点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.解抽象不等式应先将不等式化为f(m)>f(n)(f(m)<f(n))的形式.属于基础题.
函数的定义域为
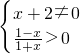 解得x∈(-1,1)
解得x∈(-1,1)∵
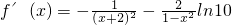 <0
<0∴f(x)在(-1,1)上递减
(II)∵f(x)与f-1(x)的单调性相同
∴f-1(x)在定义域上递减
∵
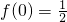
∴

∴f-1(x)=0有解,且唯一
(III)原不等式同解于

∵f(x)在(-1,1)上递减
∴
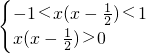 解得
解得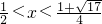 或
或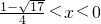
∴解集为
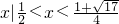 或
或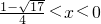 .
.分析:(I)令分母不为0且真数大于0求出函数的定义域;利用导数的运算法则求出导函数,判断出导函数的符号,得证.
(II)根据互为反函数的单调性相同,得到f-1(x)递减;求出f(0)的值,得到反函数有根,据单调证得根唯一.
(III)将
 用f(0)代替,利用f(x)的单调性去掉法则f,注意定义域;解二次不等式组求出解集.
用f(0)代替,利用f(x)的单调性去掉法则f,注意定义域;解二次不等式组求出解集.点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.解抽象不等式应先将不等式化为f(m)>f(n)(f(m)<f(n))的形式.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目