题目内容
14. 有一块直角三角形木板,如图所示,∠C=90°,AB=5cm,BC=3cm,AC=4cm.根据需要,要把它加工成一个面积最大的正方形木板,设计一个方案,应怎样裁才能使正方形木板面积最大,并求出这个正方形木板的边长.
有一块直角三角形木板,如图所示,∠C=90°,AB=5cm,BC=3cm,AC=4cm.根据需要,要把它加工成一个面积最大的正方形木板,设计一个方案,应怎样裁才能使正方形木板面积最大,并求出这个正方形木板的边长.
分析 由题意,设出正方形边长为a,根据勾股定理建立关系,利用相似三角形的性质求解边长的关系,即可求解最大值即可.
解答 解:如图(1)所示,设正方形DEFG的边长为x cm,过点C作CM⊥AB于M,交DE于N,
因为S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CM,
所以AC•BC=AB•CM,即3×4=5•CM.所以CM=$\frac{12}{5}$.
因为DE∥AB,所以△CDE∽△CAB.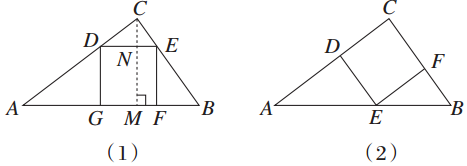
所以$\frac{CN}{CM}=\frac{DE}{AB}$,即$\frac{\frac{12}{5}-x}{\frac{12}{5}}=\frac{x}{5}$
所以x=$\frac{60}{37}$
如图(2)所示,设正方形CDEF的边长为y cm,因为EF∥AC,所以△BEF∽△BAC.
∴$\frac{BF}{BC}=\frac{EF}{AC}$,$\frac{3-x}{3}=\frac{y}{4}$.
∴y=$\frac{12}{7}$.
∵x=$\frac{60}{37}$,y=$\frac{12}{7}$,
∴x<y.
所以当按图(2)的方法裁剪时,正方形面积最大,其边长为$\frac{12}{7}$cm.
点评 本题考查的是相似三角形在实际生活中的应用,能根据题意画出图形,作出辅助线,再根据相似三角形的判定定理及性质进行解答.

练习册系列答案
相关题目
5.一个各面均涂有油漆的正方体(魔方)被锯成27个同样大小的小正方体,将这些小正方体均匀的搅混在一起,现任意的取出一个小正方体,则事件“小正方体的三个面上有油漆”的概率是( )
| A. | $\frac{12}{27}$ | B. | $\frac{6}{27}$ | C. | $\frac{1}{27}$ | D. | $\frac{8}{27}$ |
19.某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如表所示:
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)判断是否有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(2)判断是否有99.9%的把握认为学生的学习积极性与对待班级工作的态度有关系?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
6.2016年春晚过后,为了研究演员上春晚次数与受关注度的关系,某站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计,得到如下数据:
(Ⅰ)若该演员的粉丝数量y与上春晚次数x满足线性回归方程,试求回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并就此分析:该演员上春晚11次时的粉丝数量;
(Ⅱ)若用$\frac{y_i}{x_i}$(i=1,2,3,4,5)表示统计数据时粉丝的“即时均值”(精确到整数):
(1)求这5次统计数据时粉丝的“即时均值”的方差;
(2)从“即时均值”中任选2组,求这两组数据之和不超过15的概率.
参考公式:$\begin{array}{l}用最小二乘法求线性回归方程系数公式:\\ \widehatb=\frac{{\sum_{i-1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i-1}^n{x_i^2-n{{\overline x}^2}}}}=\frac{{\sum_{i-1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i-1}^n{{{({{x_i}-\overline x})}^2}}}},\widehata=\overline y-b\overline x\end{array}$.
| 上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y(单位:万人) | 10 | 20 | 40 | 80 | 100 |
(Ⅱ)若用$\frac{y_i}{x_i}$(i=1,2,3,4,5)表示统计数据时粉丝的“即时均值”(精确到整数):
(1)求这5次统计数据时粉丝的“即时均值”的方差;
(2)从“即时均值”中任选2组,求这两组数据之和不超过15的概率.
参考公式:$\begin{array}{l}用最小二乘法求线性回归方程系数公式:\\ \widehatb=\frac{{\sum_{i-1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i-1}^n{x_i^2-n{{\overline x}^2}}}}=\frac{{\sum_{i-1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i-1}^n{{{({{x_i}-\overline x})}^2}}}},\widehata=\overline y-b\overline x\end{array}$.
4.某农村合作联社欲种植一种农作物,有A、B两个品种供选择,根据前期在8块实验田中的种植试验,得出A、B两个品种的每公顷产量如下(单位:kg/hm2)
(Ⅰ)分别求出品种A和品种B的每公顷产量的样本平均数和方差;根据试验结果,你认为应该种植哪一品种;
(Ⅱ)如果联合社在一块耕地上选择种植A品种作物,其中种植成本为1000元,若根据试验得知A品种作物的市场价格和这块耕地上的产量均具有随机性且互不影响,其具体情况如表:
求在这块耕地上种植A品种作物利润为2000元的概率.
| 品种A | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| 品种B | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
(Ⅱ)如果联合社在一块耕地上选择种植A品种作物,其中种植成本为1000元,若根据试验得知A品种作物的市场价格和这块耕地上的产量均具有随机性且互不影响,其具体情况如表:
| A品种作物产量(kg) | 300 | 500 |
| 概率 | 0.5 | 0.5 |
| A品种作物市场价格(元/kg) | 6 | 10 |
| 概率 | 0.4 | 0.6 |