题目内容

在△ABC中，a、b、c分别是角A、B、C的对边，cosB=，且=-21．

(Ⅰ)求△ABC的面积；

(Ⅱ)若a=7，求角C．

答案：(Ⅰ)∵|cos(π-B)=-ac·cosB=ac=-21，

∴ac=35．

又∵cosB=，且B∈(0，π)，

∴sinB=，

∴SΔABC=ac·sinB=×35×=14

(Ⅱ)由(Ⅰ)知ac=35，又a=7，∴c=5，

b2=49+25-2×7×5×=32，∴b=，

由正弦定理得，

即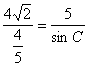，∴sinC=，

又∵a＞c，∴C∈(0，)  ∴C=.

练习册系列答案
相关题目
在△ABC中，∠A、∠B、∠C所对的边长分别是a、b、c．满足2acosC+ccosA=b．则sinA+sinB的最大值是（　　）
A、
2
2
B、1
C、
2
D、
1+
2
2
在△ABC中，a＜b＜c，B=60°，面积为10
3
cm2，周长为20cm，求此三角形的各边长．
在△ABC中，a，b，c分别为角A，B，C的对边，已知
.
m
=(cos
C
2
，sin
C
2
)，
.
n
=(cos
C
2
，-sin
C
2
)，且
m
•
n
=
1
2
．
（1）求角C；
（2）若a+b=
11
2
，△ABC的面积S=
3
3
2
，求边c的值．
在△ABC中，A，B，C为三个内角，若cotA•cotB＞1，则△ABC是（　　）
已知y=f（x）函数的图象是由y=sinx的图象经过如下三步变换得到的：
①将y=sinx的图象整体向左平移
π
6
个单位；
②将①中的图象的纵坐标不变，横坐标缩短为原来的
1
2
；
③将②中的图象的横坐标不变，纵坐标伸长为原来的2倍．
（1）求f（x）的周期和对称轴；
（2）在△ABC中，a，b，c分别是角A，B，C的对边，且f（C）=2，c=1，ab=2
3
，且a＞b，求a，b的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网