题目内容
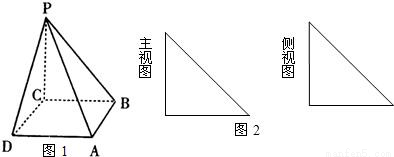
如下图,在四棱锥P—ABCD中,底面ABCD是正方形,侧面PDC是边长为a的正三角形,且平面PDC⊥底面ABCD,E为PC的中点.
(1)求异面直线PA与DE所成角的余弦值;
(2)求点D到平面PAB的距离.
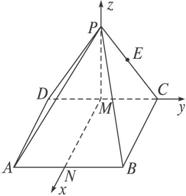
解:取DC的中点M,AB中点N,连结PM,MN,由△PDC为正三角形和PM⊥CD,又∵平面PDC⊥平面ABCD.且面PDC∩平面ABCD=CD,∴PM⊥平面ABCD,由四边形ABCD为正方形知MN⊥CD.因此以M点为原点,MN,MC,MP所在直线为x轴、y轴、z轴建立直角坐标系.

则M(0,0,0),C(0,![]() ,0),D(0,-
,0),D(0,-![]() ,0),P(0,0,
,0),P(0,0,![]() a),A(a,-
a),A(a,-![]() ,0),B(a,
,0),B(a,![]() ,0),
,0),
(1)由E为PC中点知E(0,![]() ,
,![]() a).
a).
∴![]() =(a,-
=(a,-![]() ,-
,-![]() a),
a),![]() =(0,
=(0,![]() ,
,![]() a).
a).
∴![]() ·
·![]() =-
=-![]() a2,|
a2,|![]() |=
|=![]() a,|
a,|![]() |=
|=![]() a,
a,
∴cos(![]() ,
,![]() )=
)=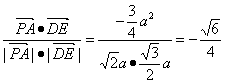 ,
,
因此异面直线PA与DE的夹角的余弦值为![]() .
.
(2)设n为平面PAB的法向量,并设n=(x,y,z),则
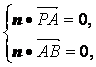
即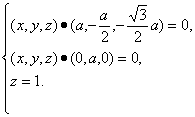
∴n=(![]() ,0,1).
,0,1).
又∵![]() =(a,0,0),
=(a,0,0),
∴d=|![]() |=
|=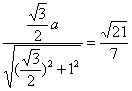 a,
a,
即点D到平面PAB的距离为![]() a.
a.

练习册系列答案
相关题目
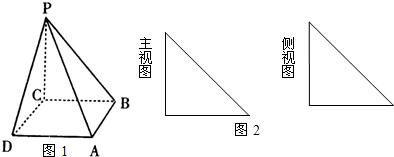
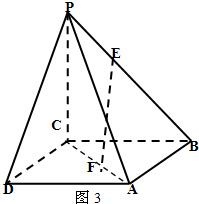
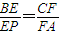 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.
 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.

 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.
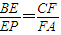 ,求证:EF∥平面PDA.
,求证:EF∥平面PDA.