题目内容
已知函数
.
(1) 求函数
的定义域
；
(2) 判断函数在定义域上的单调性，并说明理由；
（3）当
满足什么关系时，在
上恒取正值。
解析：（1）
要意义，
-----------2分
（只要学生得出答案，没有过程的，倒扣一分，用指数函数单调性或者直接解出）
所求定义域为
-----------------------------------------4分
（2）函数在定义域上是单调递增函数------------------------------5分
证明：
---------------------------------------6分
-----------------------------------------7分
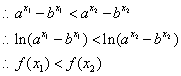-----------------------------------9分
所以原函数在定义域上是单调递增函数-------------------------10分
（3）要使
在
上恒取正值
须在上的最小值大于0--------------------------11分
由（2）
------------------------------12分
所以在上恒取正值时有
-------------------14分
练习册系列答案
阅读快车系列答案
相关题目