题目内容

已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1与该椭圆相交于P和Q,且OP⊥OQ,|PQ|=,求椭圆的方程.

解析:设椭圆方程为mx2+ny2=1(m＞0,n＞0),P(x1,y1)、Q(x2,y2),

由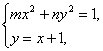消去y得(m+n)x2+2nx+n-1=0.

∴x1+x2=-,x1·x2=.

∵y1=x1+1,y2=x2+1,

∴y1·y1=(x1+1)·(x2+1)=x1·x2+(x1+x2)+1

=-.

∵OP⊥OQ,∴=-1,即x1·x2+y1·y2=0.

∴=0,得m+n=2.

∵|PQ|=,∴由弦长公式得·.

将m=2-n代入得n=或n=.

当n=时,m=;当n=时,m=.

故所求椭圆的方程为3x2+y2=2或x2+3y2=2.

练习册系列答案
相关题目
精英家教网已知椭圆的中心在坐标原点O，焦点在x轴上，短轴长为2，且两个焦点和短轴的两个端点恰为一个正方形的顶点．过右焦点F与x轴不垂直的直线l交椭圆于P，Q两点．
（1）求椭圆的方程；
（2）当直线l的斜率为1时，求△POQ的面积；
（3）在线段OF上是否存在点M（m，0），使得以MP，MQ为邻边的平行四边形是菱形？若存在，求出m的取值范围；若不存在，请说明理由．
已知椭圆的中心在坐标原点，且经过点M(1，
2
5
5
)，N(-2，
5
5
)，若圆C的圆心与椭圆的右焦点重合，圆的半径恰好等于椭圆的短半轴长，已知点A（x，y）为圆C上的一点．
（1）求椭圆的标准方程和圆的标准方程；
（2）求
AC
•
AO
+2|
AC
-
AO
|（O为坐标原点）的取值范围；
（3）求x2+y2的最大值和最小值．
已知椭圆的中心在坐标原点，焦点在x轴上，椭圆上点P(3
2
，4)到两焦点的距离之和是12，则椭圆的标准方程是
 
．
已知椭圆的中心在坐标原点，焦点在x轴上，焦距为6
3
，且椭圆上一点到两个焦点的距离之和为12，则椭圆的方程为
x2
36
+
y2
9
=1
x2
36
+
y2
9
=1
．
已知椭圆的中心在坐标原点O，焦点在x轴上，离心率为
2
2
，坐标原点O到过右焦点F且斜率为1的直线的距离为
2
2
．
（1）求椭圆的方程；
（2）设过右焦点F且与坐标轴不垂直的直线l交椭圆于P、Q两点，在线段OF上是否存在点M（m，0），使得以MP、MQ为邻边的平行四边形是菱形？若存在，求出m的取值范围；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网