题目内容
设{an}和{bn}都是公差不为零的等差数列,且
=2,则
的值为
.
| lim |
| n→∞ |
| an |
| bn |
| lim |
| n→∞ |
| b1+b2+…+bn |
| na2n |
| 1 |
| 8 |
| 1 |
| 8 |
分析:设{an}和{bn}的公差分别为d1 和d2,有条件可得d1=2d2,根据等差数列的通项公式及前n项和公式化简要求的式子
并把d1=2d2代入,再利用数列极限的运算法则求出结果.
并把d1=2d2代入,再利用数列极限的运算法则求出结果.
解答:解:设{an}和{bn}的公差分别为d1 和d2,
∵
=
=
=2,∴d1=2d2.
=
=
=
=
,
故答案为:
.
∵
| lim |
| n→∞ |
| an |
| bn |
| lim |
| n→∞ |
| a1+(n-1)d1 |
| b1+(n-1)d2 |
| d1 |
| d2 |
| lim |
| n→∞ |
| b1+b2+…+bn |
| na2n |
| lim |
| n→∞ |
nb1+
| ||
| n[a1+(2n-1)d1 ] |
| ||
| 2×d1 |
| d2 |
| 4d1 |
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |
点评:本题主要考查等差数列的通项公式,前n项和公式,求数列的极限的方法,得到d1=2d2,是解题的关键.

练习册系列答案
相关题目
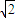 ,|β|>2
,|β|>2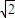
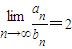 ,则
,则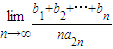 的值为 .
的值为 .