题目内容
已知定义在区间 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线 对称,当
对称,当 时,函数
时,函数 ,其图象如图.
,其图象如图.
(1)求函数y=f(x)在 的表达式;
的表达式;
(2)求方程 的解.
的解.

解:(1)当 时,
时,
函数 ,观察图象易得:A=1,周期为2π,可得ω=1,
,观察图象易得:A=1,周期为2π,可得ω=1,
再将点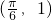 代入,结合题设可得φ=
代入,结合题设可得φ= ,即函数
,即函数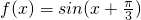 ,
,
由函数y=f(x)的图象关于直线 对称得,
对称得, 时,函数f(x)=-sinx.
时,函数f(x)=-sinx.
∴ .
.
(2)当 时,
时,
由 得,
得, ;
;
当 时,由
时,由 得,
得, .
.
∴方程 的解集为
的解集为
分析:(1)观察图象易得当 时,:
时,: ,再由函数y=f(x)的图象关于直线
,再由函数y=f(x)的图象关于直线 对称求出
对称求出 上的解析式,即可得到函数y=f(x)在
上的解析式,即可得到函数y=f(x)在 的表达式;
的表达式;
(2)由(1)函数的解析式是一个分段函数,故分段解方程求方程 的解.
的解.
点评:本题考查由函数的部分图象求函数的解析式,解题的关键是熟练掌握三角函数图象的特征,根据这些特征求出解析式中的系数,得出函数的解析式,本题涉及到函数的对称性求解析式,以及解三角方程,运算量较大,易因运算导致错误,解题时要谨慎.
 时,
时,函数
 ,观察图象易得:A=1,周期为2π,可得ω=1,
,观察图象易得:A=1,周期为2π,可得ω=1,再将点
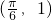 代入,结合题设可得φ=
代入,结合题设可得φ= ,即函数
,即函数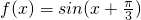 ,
,由函数y=f(x)的图象关于直线
 对称得,
对称得, 时,函数f(x)=-sinx.
时,函数f(x)=-sinx.∴
 .
.(2)当
 时,
时,由
 得,
得, ;
;当
 时,由
时,由 得,
得, .
.∴方程
 的解集为
的解集为
分析:(1)观察图象易得当
 时,:
时,: ,再由函数y=f(x)的图象关于直线
,再由函数y=f(x)的图象关于直线 对称求出
对称求出 上的解析式,即可得到函数y=f(x)在
上的解析式,即可得到函数y=f(x)在 的表达式;
的表达式;(2)由(1)函数的解析式是一个分段函数,故分段解方程求方程
 的解.
的解.点评:本题考查由函数的部分图象求函数的解析式,解题的关键是熟练掌握三角函数图象的特征,根据这些特征求出解析式中的系数,得出函数的解析式,本题涉及到函数的对称性求解析式,以及解三角方程,运算量较大,易因运算导致错误,解题时要谨慎.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 ,满足
,满足 ,且在区间[0,2]上是增函
,且在区间[0,2]上是增函 B.
B.

 D.
D.

 ,满足
,满足 ,且在区间[0,1]上是增函
,且在区间[0,1]上是增函 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则 ( )
( ) (B)
(B) (C)
(C)  (D)
(D)