题目内容
【题目】已知关于![]() 的函数
的函数![]() 为
为![]() 上的偶函数,且在区间
上的偶函数,且在区间![]() 上的最大值为10. 设
上的最大值为10. 设![]() .
.
⑴ 求函数![]() 的解析式;
的解析式;
⑵ 若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
⑶ 是否存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有四个不相等的实 数根?如果存在,求出实数
有四个不相等的实 数根?如果存在,求出实数![]() 的范围,如果不存在,说明理由.
的范围,如果不存在,说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】【试题分析】(1)利用![]() ,化简后可求得
,化简后可求得![]() .此时函数对称轴为
.此时函数对称轴为![]() 轴,故当
轴,故当![]() 时取得最大值,由此求得
时取得最大值,由此求得![]() .进而求得
.进而求得![]() .(2)将原不等式分离参数得到
.(2)将原不等式分离参数得到![]() 在
在![]() 上恒成立,利用换元法结合二次函数最值可求得
上恒成立,利用换元法结合二次函数最值可求得![]() .(3)先将原方程化为
.(3)先将原方程化为![]() .利用换元法令
.利用换元法令![]() ,将上式变为二次函数零点问题来求解.
,将上式变为二次函数零点问题来求解.
【试题解析】
(1)∵![]() 为
为![]() 上的偶函数,
上的偶函数, ![]() ,
,
![]() ,
, ![]() 关于
关于![]() 恒成立,
恒成立, ![]()
![]() ,
, ![]() 在区间
在区间![]() 上的最大值为10,
上的最大值为10,
![]() 当
当![]() 时,
时, ![]() 解得:
解得: ![]() ,
,
![]()
![]()
(2)不等式![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
上式可化为![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,∵
,∵![]() ,∴
,∴![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
又∵当![]() 时,
时, ![]() ,∴
,∴![]() ,即所求实数
,即所求实数![]() 的取值范围为
的取值范围为![]()
(3)方程![]() ,即
,即![]() ,
,
可化为: ![]() ,
,
令![]() ,则
,则![]() ,
,
若关于![]() 的方程
的方程![]() 有四个不相等的实数根,
有四个不相等的实数根,
则关于![]() 的方程
的方程![]() 必须有两个不相等的实数根
必须有两个不相等的实数根![]() 和
和![]() ,
,
并且![]() ,记
,记![]()
![]() ,
,
则, 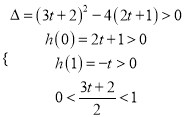
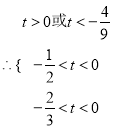 解得:
解得: ![]() ,所以,存在实数
,所以,存在实数![]() 使得关于
使得关于![]() 的方程
的方程
![]() 有四个不相等的实数根,
有四个不相等的实数根, ![]() 取值范围为
取值范围为![]()

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目