题目内容
已知数列{an}的前n项和为Sn,且满足
an+2Sn•Sn﹣1=0(n≥2),a1=![]() .
.
(1)求证:{![]() }是等差数列;
}是等差数列;
(2)求an表达式;
(3)若bn=2(1﹣n)an(n≥2),求证:b22+b32+…+bn2<1.
考点:
数列递推式;等差关系的确定;数列的求和.
专题:
计算题;证明题.
分析:
(1)根据题中已知条件化简可得出Sn与Sn﹣1的关系,再求出S1 的值即可证明{![]() }是等差数列;
}是等差数列;
(2)根据(1)中求得的Sn与Sn﹣1的关系先求出数列{![]() }的通项公式,然后分别讨论n=1和n≥2时an的表达式;
}的通项公式,然后分别讨论n=1和n≥2时an的表达式;
(3)根据(2)中求得的an的表达式即可求出bn的表达式,然后将bn的表达式代入b22+b32+…+bn2中,利用缩放法即可证明b22+b32+…+bn2<1.
解答:
解(1)∵﹣an=2SnSn﹣1,
∴﹣Sn+Sn﹣1=2SnSn﹣1(n≥2)
Sn≠0,∴![]() ﹣
﹣![]() =2,又
=2,又![]() =
=![]() =2,
=2,
∴{![]() }是以2为首项,公差为2的等差数列.(2)由(1)
}是以2为首项,公差为2的等差数列.(2)由(1)![]() =2+(n﹣1)2=2n,
=2+(n﹣1)2=2n,
∴Sn=![]()
当n≥2时,an=Sn﹣Sn﹣1=﹣![]()
n=1时,a1=S1=![]() ,
,
∴an=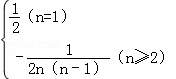 ;(3)由(2)知bn=2(1﹣n)an=
;(3)由(2)知bn=2(1﹣n)an=![]()
∴b22+b32+…+bn2=![]() +
+![]() +…+
+…+![]() <
<![]() +
+![]() +…+
+…+![]()
=(1﹣![]() )+(
)+(![]() ﹣
﹣![]() )+…+(
)+…+(![]() ﹣
﹣![]() )=1﹣
)=1﹣![]() <1.
<1.
点评:
本题主要考查了数列的递推公式以及等差数列的基本性质,考查了学生的计算能力和对数列的综合掌握,解题时注意整体思想和转化思想的运用,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |