题目内容
已知函数 ,(a>0),x∈(0,b),则下列判断正确的是
,(a>0),x∈(0,b),则下列判断正确的是
- A.当
 时,f(x)的最小值为
时,f(x)的最小值为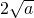
- B.当
 时,f(x)的最小值为
时,f(x)的最小值为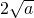
- C.当
 时,f(x)的最小值为
时,f(x)的最小值为
- D.对任意的b>0,f(x)的最小值均为
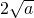
A
分析:通过观察可知,已知解析式可整理成基本不等式的形式,然后根据等号能否取到分情况讨论求解.
解答:∵ =x+
=x+ ,
,
∴当 时,f(x)≥
时,f(x)≥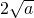 ,
,
当且仅当x= ,即x=
,即x= 时取等号;
时取等号;
当 时,y=f(x)在(0,b)上单调递减,
时,y=f(x)在(0,b)上单调递减,
∴f(x)< ,故f(x)不存在最小值;
,故f(x)不存在最小值;
故选A.
点评:利用基本不等式求最值或证明不等式时,应满足一正、二定、三相等这三个条件,否则会出错.
分析:通过观察可知,已知解析式可整理成基本不等式的形式,然后根据等号能否取到分情况讨论求解.
解答:∵
 =x+
=x+ ,
,∴当
 时,f(x)≥
时,f(x)≥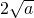 ,
,当且仅当x=
 ,即x=
,即x= 时取等号;
时取等号;当
 时,y=f(x)在(0,b)上单调递减,
时,y=f(x)在(0,b)上单调递减,∴f(x)<
 ,故f(x)不存在最小值;
,故f(x)不存在最小值;故选A.
点评:利用基本不等式求最值或证明不等式时,应满足一正、二定、三相等这三个条件,否则会出错.

练习册系列答案
相关题目
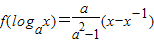 ,其中a>0且a≠1.
,其中a>0且a≠1. ,其中a>0.
,其中a>0.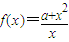 ,(a>0),x∈(0,b),则下列判断正确的是( )
,(a>0),x∈(0,b),则下列判断正确的是( )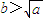 时,f(x)的最小值为
时,f(x)的最小值为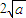
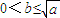 时,f(x)的最小值为
时,f(x)的最小值为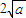
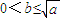 时,f(x)的最小值为
时,f(x)的最小值为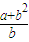
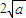
 +bx(a>0)且f′(1)=0,
+bx(a>0)且f′(1)=0,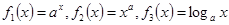 (其中a>0,且a≠),在同一坐标系中画出其中两个函数在第一象限内的图像,其中正确的是
(其中a>0,且a≠),在同一坐标系中画出其中两个函数在第一象限内的图像,其中正确的是