题目内容
在 中,
中, ,
, ,
, ,若点
,若点 满足
满足 ,且
,且 ,则
,则 = .
= .

解析试题分析:由题意点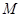 在直线
在直线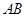 上,
上,
 ,
,
则 ,即
,即 ,所以点
,所以点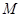 在
在 延长线上,由
延长线上,由 ,得
,得 ,因此
,因此 ,在
,在 中由余弦定理得
中由余弦定理得 ,再由余弦定理得
,再由余弦定理得 .
.
考点:共线向量定理,向量的数量积,余弦定理.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
题目内容
在 中,
中, ,
, ,
, ,若点
,若点 满足
满足 ,且
,且 ,则
,则 = .
= .

解析试题分析:由题意点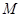 在直线
在直线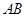 上,
上,
 ,
,
则 ,即
,即 ,所以点
,所以点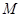 在
在 延长线上,由
延长线上,由 ,得
,得 ,因此
,因此 ,在
,在 中由余弦定理得
中由余弦定理得 ,再由余弦定理得
,再由余弦定理得 .
.
考点:共线向量定理,向量的数量积,余弦定理.

 发散思维新课堂系列答案
发散思维新课堂系列答案