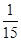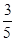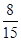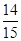题目内容
在平面直角坐标系 中,平面区域
中,平面区域 中的点的坐标
中的点的坐标 满足
满足 , 从区域
, 从区域 中随机取点
中随机取点 .
.
(Ⅰ)若
 ,
, ,点
,点 位于第一象限的概率是 ;
位于第一象限的概率是 ;
(Ⅱ)若
 ,
, ,
,  的概率是 .
的概率是 .
 中,平面区域
中,平面区域 中的点的坐标
中的点的坐标 满足
满足 , 从区域
, 从区域 中随机取点
中随机取点 .
.(Ⅰ)若

 ,
, ,点
,点 位于第一象限的概率是 ;
位于第一象限的概率是 ;(Ⅱ)若

 ,
, ,
,  的概率是 .
的概率是 . ;
; ;
;(1)平面区域 中的点的坐标
中的点的坐标 满足
满足 的整点共有12个:(—1,0)(—1,1)(—1,2),(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)。其中位于第一象限的有(1,1),(1,2),(2,1),(2,2)等4个,所以点
的整点共有12个:(—1,0)(—1,1)(—1,2),(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)。其中位于第一象限的有(1,1),(1,2),(2,1),(2,2)等4个,所以点 位于第一象限的概率是
位于第一象限的概率是 。
。
(2)平面区域 中的点的坐标
中的点的坐标 满足
满足
所构成矩形的面积为6,其中满足 的区域面积为圆心角为
的区域面积为圆心角为 的扇形面积及一个含锐角
的扇形面积及一个含锐角 的直角三角形面积之和:
的直角三角形面积之和: ,所以
,所以 的概率是
的概率是 .
.
 中的点的坐标
中的点的坐标 满足
满足 的整点共有12个:(—1,0)(—1,1)(—1,2),(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)。其中位于第一象限的有(1,1),(1,2),(2,1),(2,2)等4个,所以点
的整点共有12个:(—1,0)(—1,1)(—1,2),(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)。其中位于第一象限的有(1,1),(1,2),(2,1),(2,2)等4个,所以点 位于第一象限的概率是
位于第一象限的概率是 。
。(2)平面区域
 中的点的坐标
中的点的坐标 满足
满足
所构成矩形的面积为6,其中满足
 的区域面积为圆心角为
的区域面积为圆心角为 的扇形面积及一个含锐角
的扇形面积及一个含锐角 的直角三角形面积之和:
的直角三角形面积之和: ,所以
,所以 的概率是
的概率是 .
.
练习册系列答案
相关题目
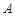 往
往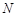 走,且只能向右或向下走,随机地选一种走法,则经过点
走,且只能向右或向下走,随机地选一种走法,则经过点 的概率是 .
的概率是 .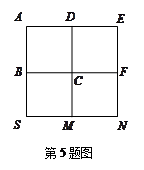
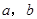 )是平面上的一个点,设事件A表示“
)是平面上的一个点,设事件A表示“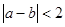 ”,其中
”,其中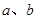 为实常数.
为实常数. 中不放回地依次取
中不放回地依次取 个数,事件
个数,事件 “第一次取到的是奇数”,
“第一次取到的是奇数”, “第二次取到的是奇数”,则
“第二次取到的是奇数”,则




 的数学期望。
的数学期望。