题目内容
9．设Sn=1+3+5+…+（2n-1）（n∈N*），则f（n）=$\frac{（n+8）（n+2）}{\sqrt{{S}_{n}}}$的最小值为（ ）| A． | 9 | B． | 12 | C． | 18 | D． | 24 |
分析 由等差数列的前n项和求得Sn，代入f（n）=$\frac{（n+8）（n+2）}{\sqrt{{S}_{n}}}$后利用基本不等式求最值．
解答 解：∵Sn=1+3+5+…+（2n-1）=$\frac{（1+2n-1）n}{2}={n}^{2}$，
∴f（n）=$\frac{（n+8）（n+2）}{\sqrt{{S}_{n}}}$=$\frac{{n}^{2}+10n+16}{n}=n+\frac{16}{n}+10$$≥2\sqrt{n•\frac{16}{n}}+10=18$．
上式当且仅当n=4时取等号．
故选：C．
点评 本题考查等差数列的前n项和，考查了利用基本不等式求最值，是基础题．
练习册系列答案
相关题目
12．设A，B是双曲线x2-y2=1上关于原点O对称的两点，将坐标平面沿双曲线的一条渐近线l折成直二面角，则折叠后线段AB长度的最小值为（ ）
| A． | $\sqrt{2\sqrt{2}}$ | B． | $\sqrt{3\sqrt{2}}$ | C． | $\sqrt{2}$ | D． | 3 |
20．假如今年省运会给岭师附中高中三个年级7个自主推荐的志愿者名额，则每个年级至少分到一个名额的方法数为（ ）
| A． | 10 | B． | 15 | C． | 21 | D． | 30 |
17．直线y=m分别与曲线y=2x+3，y=x+lnx交于A、B，则|AB|的最小值为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{3\sqrt{2}}{4}$ | C． | 2 | D． | 3 |
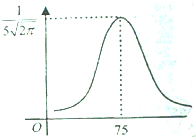某市高二理科学生数学考试的成绩x服从正态分布，其密度函数为f（x）=$\frac{1}{\sqrt{2π}σ}$e${\;}^{\frac{（x-μ）^{2}}{2{σ}^{2}}}$，密度曲线如图，已知该市理科学生总数是10000人，则成绩位于（65，85]的人数约是9544．