题目内容
如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3，PB=2，PC=1，设M是底面ABC内的点，定义f（M）=（m，n，p），其中m，n，p分别是三棱锥M-PAB，三棱锥M-BPC、三棱锥M-PCA的体积．若f（M）=（
，x，y），则
最小值为________．
8
分析：由图可知：V三棱锥P-ABM+V三棱锥P-BCM+V三棱锥P-ACM=V三棱锥P-ABC，进而得出
，再利用基本不等式的性质即可．
解答：由图可知：V三棱锥P-ABM+V三棱锥P-BCM+V三棱锥P-ACM=V三棱锥P-ABC，
∴
，
∴．（x＞0，y＞0）．
∴=
=2
=8，当且仅当
，即x=y=
时取等号．
故答案为8．
点评：由已知得出x+y=和利用基本不等式的性质是解题的关键．
分析：由图可知：V三棱锥P-ABM+V三棱锥P-BCM+V三棱锥P-ACM=V三棱锥P-ABC，进而得出
，再利用基本不等式的性质即可．解答：由图可知：V三棱锥P-ABM+V三棱锥P-BCM+V三棱锥P-ACM=V三棱锥P-ABC，
∴
，∴
．（x＞0，y＞0）．∴
==2=8，当且仅当，即x=y=时取等号．故答案为8．
点评：由已知得出x+y=
和利用基本不等式的性质是解题的关键． 
练习册系列答案
名校课堂系列答案
相关题目
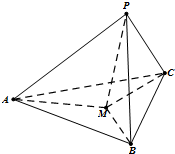如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3．PB=2，PC=1．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f（M）=（
如图，在三棱锥P-ABC中，PA⊥底面ABC，∠ACB=90°，AE⊥PB于E，AF⊥PC于F，若PA=AB=2，∠BPC=θ，则当△AEF的面积最大时，tanθ的值为（ ）
如图，在三棱锥P-ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D、E分别为AB、AC中点．
如图，在三棱锥P-ABC中，已知PA=PB=PC，∠BPA=∠BPC=∠CPA=40°，一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是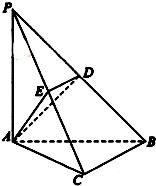
如图，在三棱锥P-ABC中，PA⊥底面ABC，∠BCA=90°，AP=AC，点D，E分别在棱