题目内容
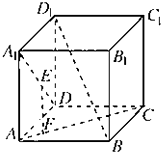 棱长为a的正方体ABCD-A1B1C1D1中,EF是异面直线AC与AD1的公垂线,
棱长为a的正方体ABCD-A1B1C1D1中,EF是异面直线AC与AD1的公垂线,求证:EF∥BD1.
分析:建立空间直角坐标系,设出点的坐标,得出向量坐标,证明
∥
,可得结论.
| BD1 |
| EF |
解答: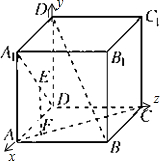 证明:如图,以D为原点建立空间直角坐标系D-xyz,
证明:如图,以D为原点建立空间直角坐标系D-xyz,
设正方体的棱长为a,则A1(a,0,a),D(0,0,0),A(a,0,0),C(0,a,0),B(a,a,0),D1(0,0,a),
∴
1=(a,0,a),
=(-a,a,0),
1=(-a,-a,a).
∵EF是直线AC与A1D的公垂线.
∴
⊥
1,
⊥
.
设
=(x,y,z),
∴
•
1=(x,y,z)•(a,0,a)=ax+az=0,
∴
•
=(x,y,z)•(-a,a,0)=-ax+ay=0.
∵a≠0,∴x=y=-z.
∴
=(x,x,-x),∴
1=-
,
∴
∥
,
∴EF∥BD1.
 证明:如图,以D为原点建立空间直角坐标系D-xyz,
证明:如图,以D为原点建立空间直角坐标系D-xyz,设正方体的棱长为a,则A1(a,0,a),D(0,0,0),A(a,0,0),C(0,a,0),B(a,a,0),D1(0,0,a),
∴
| DA |
| AC |
| BD |
∵EF是直线AC与A1D的公垂线.
∴
| EF |
| DA |
| EF |
| AC |
设
| EF |
∴
| EF |
| DA |
∴
| EF |
| AC |
∵a≠0,∴x=y=-z.
∴
| EF |
| BD |
| a |
| x |
| EF |
∴
| BD1 |
| EF |
∴EF∥BD1.
点评:本题考查线线平行,考查向量知识的运用,正确确定向量坐标是关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
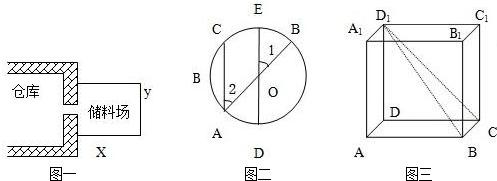
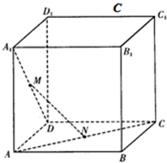 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.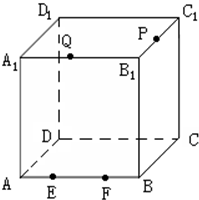 在棱长为a的正方体ABCD-A1B1C1D1中,P是C1B1的中点,若E,F都是AB上的点,且
在棱长为a的正方体ABCD-A1B1C1D1中,P是C1B1的中点,若E,F都是AB上的点,且 (2001•上海)在棱长为a的正方体OABC-O′A′B′C′中,E、F分别是棱AB、BC上的动点,且AE=BF.
(2001•上海)在棱长为a的正方体OABC-O′A′B′C′中,E、F分别是棱AB、BC上的动点,且AE=BF.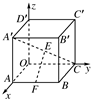 如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为( )
如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为( )