��Ŀ����
����Ŀ��ij�̳������н���������˿���һ��������Ʒ�ɳ齱���齱�������£�1���齱�������������֣�����![]() ����װ��1������2��������ɫ��ͬ���ļ״����������1�������Ǻ������ý���15Ԫ������û�н��𣬶ҽ�����������Żؼ״��У�����
����װ��1������2��������ɫ��ͬ���ļ״����������1�������Ǻ������ý���15Ԫ������û�н��𣬶ҽ�����������Żؼ״��У�����![]() ����װ��2���졢1��������ɫ��ͬ�����Ҵ����������1�������Ǻ������ý���10Ԫ������û�н��𣬶ҽ�����������Ż��Ҵ��С�
����װ��2���졢1��������ɫ��ͬ�����Ҵ����������1�������Ǻ������ý���10Ԫ������û�н��𣬶ҽ�����������Ż��Ҵ��С�
�齱�����ǣ��˿�����Ʒ�Ľ����100Ԫ���ɸ��ݷ���![]() �齱һ������150Ԫ���ɸ��ݷ���
�齱һ������150Ԫ���ɸ��ݷ���![]() �齱������ij�˿�����Ʒ�Ľ��Ϊ310Ԫ����ù˿Ͳ��õij齱��ʽ�������������֣����ݷ���
�齱������ij�˿�����Ʒ�Ľ��Ϊ310Ԫ����ù˿Ͳ��õij齱��ʽ�������������֣����ݷ���![]() �齱���λ�
�齱���λ�![]() �齱���λ�
�齱���λ�![]() ���齱һ�Σ�����֪�˿�
���齱һ�Σ�����֪�˿�![]() �ڸ��̳�������Ʒ�Ľ��Ϊ250Ԫ��
�ڸ��̳�������Ʒ�Ľ��Ϊ250Ԫ��
��1�����˿�![]() ֻѡ����ݷ���
ֻѡ����ݷ���![]() ���г齱����������Ϊ15Ԫ�ĸ��ʣ�
���г齱����������Ϊ15Ԫ�ĸ��ʣ�
��2�������˿�![]() ����ÿ�ֳ齱��ʽ�Ŀ����Զ���ȣ��������п��ܻ�õĽ�������0Ԫ���⣩��
����ÿ�ֳ齱��ʽ�Ŀ����Զ���ȣ��������п��ܻ�õĽ�������0Ԫ���⣩��
���𰸡�(1) ![]() ��(2)15Ԫ.
��(2)15Ԫ.
�����������������
(1)�������г����п��ܵ��¼���Ȼ���Ϲŵ���ͼ��㹫ʽ�ɵ�����Ϊ15Ԫ�ĸ�����![]() ��
��
(2)������������ַ����������ۿɵ������п��ܻ�õĽ�������15Ԫ.
���������
��1���Ǽ״��к�����![]() ������ֱ�Ϊ
������ֱ�Ϊ![]()
������ù˿�![]() ���ԴӼ״����Ⱥ�����2���������еȿ��ܳ��ֵĽ��Ϊ
���ԴӼ״����Ⱥ�����2���������еȿ��ܳ��ֵĽ��Ϊ
![]() ��9�֣�
��9�֣�
���н��![]() �ɻ�15Ԫ�����Թ˿�
�ɻ�15Ԫ�����Թ˿�![]() ����Ϊ15Ԫ�ĸ���Ϊ
����Ϊ15Ԫ�ĸ���Ϊ![]() .
.
��2��������Ĺ˿�![]() ���Ը��ݷ���
���Ը��ݷ���![]() �齱���λ���ݷ���
�齱���λ���ݷ���![]() ���齱һ�Ρ��ɣ�1��֪�˿�
���齱һ�Ρ��ɣ�1��֪�˿�![]() ���ݷ���
���ݷ���![]() �齱����������������1��
�齱����������������1��
���Ҵ��к���ֱ���![]() ������
������![]()
��˿�![]() ���ݷ���
���ݷ���![]() ���齱һ�ε����еȿ��ܳ��ֵĽ��Ϊ
���齱һ�ε����еȿ��ܳ��ֵĽ��Ϊ
![]() ��9��
��9��
���н��![]() �ɻ�25Ԫ�����
�ɻ�25Ԫ�����![]() �ɻ�15Ԫ��
�ɻ�15Ԫ��
![]() �ɻ�10Ԫ������ɻ�0Ԫ�����Թ˿�
�ɻ�10Ԫ������ɻ�0Ԫ�����Թ˿�![]() ���ݷ���
���ݷ���![]() ���齱һ��������������2��
���齱һ��������������2��

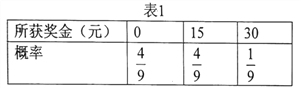
�ɱ�1����2��֪�˿�![]() ���п��ܻ�õĽ�����Ϊ15Ԫ.
���п��ܻ�õĽ�����Ϊ15Ԫ.