题目内容
已知函数y=
 (2≤x≤4)
(2≤x≤4)(1)当x=
 时,求y的值.
时,求y的值.(2)令t=log2x,求y关于t的函数关系式.
(3)求该函数的值域.
【答案】分析:(1)当)x=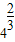 时,log2x=
时,log2x= ,代入y=
,代入y=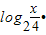
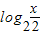 =(log2x-2)•(log2x-1)可得答案;
=(log2x-2)•(log2x-1)可得答案;
(2)若t=log2x,(2≤x≤4),则1≤t≤2,代入y=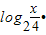
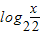 =(log2x-2)•(log2x-1)可得y关于t的函数关系式.
=(log2x-2)•(log2x-1)可得y关于t的函数关系式.
(3)分析y=t2-3t+2的图象形状,结合1≤t≤2,由二次函数的图象和性质,可求出函数的最值,进而得到函数的值域.
解答:解:(1)x=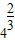 =
=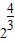 时,log2x=
时,log2x=
∴y=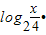
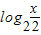
=(log2x-log24)•(log2x-log22)
=(log2x-2)•(log2x-1)
=- •
• =-
=-
(2)若t=log2x,(2≤x≤4)
则1≤t≤2,
则y=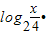
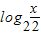
=(log2x-2)•(log2x-1)
=(t-2)•(t-1)
=t2-3t+2(1≤t≤2)
(3)∵y=t2-3t+2的图象是开口朝上,且以t= 为对称轴的抛物线
为对称轴的抛物线
又∵1≤t≤2
∴当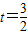 时,
时,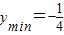
当t=1或2时,ymax=0
故函数的值域是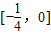
点评:本题考查的知识点是函数解析式的求法,函数的值域,函数的值,熟练掌握换元法求函数解析式及二次函数的图象和性质是解答的关键.
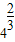 时,log2x=
时,log2x= ,代入y=
,代入y=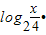
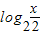 =(log2x-2)•(log2x-1)可得答案;
=(log2x-2)•(log2x-1)可得答案;(2)若t=log2x,(2≤x≤4),则1≤t≤2,代入y=
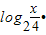
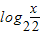 =(log2x-2)•(log2x-1)可得y关于t的函数关系式.
=(log2x-2)•(log2x-1)可得y关于t的函数关系式.(3)分析y=t2-3t+2的图象形状,结合1≤t≤2,由二次函数的图象和性质,可求出函数的最值,进而得到函数的值域.
解答:解:(1)x=
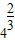 =
=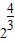 时,log2x=
时,log2x=
∴y=
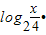
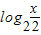
=(log2x-log24)•(log2x-log22)
=(log2x-2)•(log2x-1)
=-
 •
• =-
=-
(2)若t=log2x,(2≤x≤4)
则1≤t≤2,
则y=
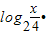
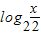
=(log2x-2)•(log2x-1)
=(t-2)•(t-1)
=t2-3t+2(1≤t≤2)
(3)∵y=t2-3t+2的图象是开口朝上,且以t=
 为对称轴的抛物线
为对称轴的抛物线又∵1≤t≤2
∴当
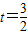 时,
时,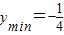
当t=1或2时,ymax=0
故函数的值域是
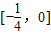
点评:本题考查的知识点是函数解析式的求法,函数的值域,函数的值,熟练掌握换元法求函数解析式及二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目