题目内容
设f(x)= +xlnx,g(x)=x3-x2-3.
+xlnx,g(x)=x3-x2-3.
(1)当a=2时,求曲线y=f(x)在x=1处的切线方程;
(2)如果存在x1,x2∈[0,2],使得g(x1)- g(x2)≥M成立,求满足上述条件的最大整数M;
(3)如果对任意的s,t∈[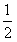 ,2],都有f(s)≥g(t)成立,求实数a的取值范围.
,2],都有f(s)≥g(t)成立,求实数a的取值范围.
 +xlnx,g(x)=x3-x2-3.
+xlnx,g(x)=x3-x2-3.(1)当a=2时,求曲线y=f(x)在x=1处的切线方程;
(2)如果存在x1,x2∈[0,2],使得g(x1)- g(x2)≥M成立,求满足上述条件的最大整数M;
(3)如果对任意的s,t∈[
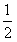 ,2],都有f(s)≥g(t)成立,求实数a的取值范围.
,2],都有f(s)≥g(t)成立,求实数a的取值范围. 解:(1)
所以,曲线y=f(x)在x=1处的切线方程为y=-x+3;
(2)

由下表知, ,
,

∴ ,
,
所以满足条件的最大整数M=4;
(3)
等价于:在区间 上,函数f(x)的最小值不小于g(x)的最大值,
上,函数f(x)的最小值不小于g(x)的最大值,
由(2)知,在区间 上,g(x)的最大值为
上,g(x)的最大值为 ,
, ,
,
下证当a≥1时,在区间 上,函数f(x)≥1恒成立,
上,函数f(x)≥1恒成立,
当a≥1且 时,
时, ,
,
记 ,
, ,
, 。
。
当 时,
时, ;
;
当 时,
时, ,
,
所以,函数在 区间
区间 上递减,在区间
上递减,在区间 上递增,
上递增, ,即h(x)≥1, 所以,当a≥1且
,即h(x)≥1, 所以,当a≥1且 时,f(x)≥1成立,
时,f(x)≥1成立,
即对任意 ,都有f(s)≥g(t)。
,都有f(s)≥g(t)。

所以,曲线y=f(x)在x=1处的切线方程为y=-x+3;
(2)


由下表知,
 ,
,
∴
 ,
,所以满足条件的最大整数M=4;
(3)

等价于:在区间
 上,函数f(x)的最小值不小于g(x)的最大值,
上,函数f(x)的最小值不小于g(x)的最大值, 由(2)知,在区间
 上,g(x)的最大值为
上,g(x)的最大值为 ,
, ,
,下证当a≥1时,在区间
 上,函数f(x)≥1恒成立,
上,函数f(x)≥1恒成立,当a≥1且
 时,
时, ,
,记
 ,
, ,
, 。
。当
 时,
时, ;
;当
 时,
时, ,
,所以,函数在
 区间
区间 上递减,在区间
上递减,在区间 上递增,
上递增, ,即h(x)≥1, 所以,当a≥1且
,即h(x)≥1, 所以,当a≥1且 时,f(x)≥1成立,
时,f(x)≥1成立,即对任意
 ,都有f(s)≥g(t)。
,都有f(s)≥g(t)。 
练习册系列答案
相关题目
 ,求证
,求证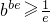 (e是自然对数的底数);
(e是自然对数的底数);