题目内容
已知数列 的前
的前 项和
项和 满足
满足 ,
,
(Ⅰ)求数列 的前三项
的前三项
(Ⅱ)设 ,求证:数列
,求证:数列 为等比数列,并指出
为等比数列,并指出 的通项公式。
的通项公式。
【答案】
(Ⅰ) 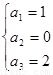 ;(Ⅱ)
;(Ⅱ)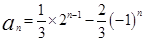 .
.
【解析】
试题分析:(Ⅰ) 求数列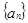 的前三项
的前三项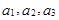 ,在
,在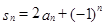 中分别令
中分别令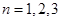 即可求出
即可求出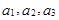 ;(Ⅱ)数列
;(Ⅱ)数列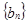 为等比数列,只需证明
为等比数列,只需证明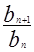 等于一个与
等于一个与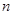 无关的常数,由
无关的常数,由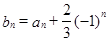 ,首先求出数列
,首先求出数列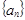 的通项公式,或递推式,由
的通项公式,或递推式,由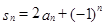 ,这是已知
,这是已知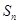 ,求
,求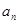 ,可利用
,可利用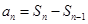 来求,即当
来求,即当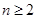 ,
,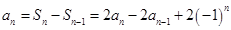 ,可得
,可得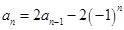 ,由
,由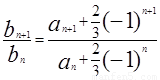 ,把
,把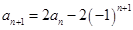 代入可得
代入可得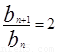 ,从而可证,求
,从而可证,求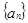 的通项公式,由
的通项公式,由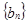 是首项为
是首项为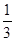 ,公比为2的等比数列,可写出
,公比为2的等比数列,可写出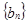 的通项公式,从而可得数列
的通项公式,从而可得数列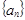 的通项公式.
的通项公式.
试题解析:(Ⅰ)在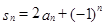 中分别令n=1,2,3得
中分别令n=1,2,3得
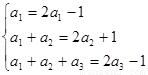 (2分)
解得
(2分)
解得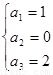 (4分)
(4分)
⑵由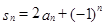 ,n≥1得
,n≥1得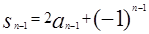 ,n≥2
,n≥2
两式想减得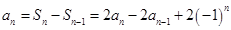 ,即
,即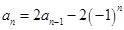 , (6分)
, (6分)
∴an+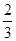 (-1)n=2an-1+
(-1)n=2an-1+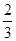 (-1)n-2(-1)n=2an-1+
(-1)n-2(-1)n=2an-1+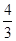 (-1)n-1
(-1)n-1
=2[an-1+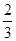 (-1)n-1](n≥2) (9分)
(-1)n-1](n≥2) (9分)
即bn=2bn-1(n≥2),b1=a1-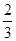 =
=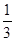
∴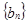 是首项为
是首项为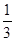 ,公比为2的等比数列.
(10分)
,公比为2的等比数列.
(10分)
∴bn=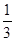 ×2n-1= an+
×2n-1= an+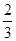 (-1)n
(-1)n
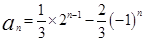 (12分)
(12分)
考点:等比数列的判断,求通项公式.

练习册系列答案
相关题目
 的前
的前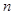 项和
项和 满足:
满足: ,且
,且 ,那么
,那么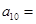 ( )
( ) 的前
的前 项和
项和 满足
满足 ,等差数列
,等差数列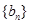 满足
满足 ,
, 。
。 ,数列
,数列 的前
的前 ,问
,问 >
> 的最小正整数
的最小正整数