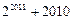题目内容
定义在R上的偶函数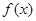 满足
满足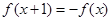 ,且在[-1,0]上单调递增,
,且在[-1,0]上单调递增,
设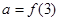 ,
,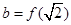 ,
,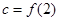 ,则
,则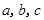 的大小关系是( )
的大小关系是( )
A. | B.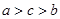  | C.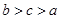  | D.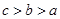 |
D
解析考点:函数单调性的性质;函数奇偶性的性质;函数的周期性.
专题:计算题.
分析:先根据条件推断出函数为以2为周期的函数,根据f(x)是偶函数,在[-1,0]上单调递增推断出在[0,1]上是减函数.减函数,进而利用周期性使a=f(1),b=f(2- 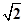 ),c=f(2)=f(0)进而利用自变量的大小求得函数的大小,则a,b,c的大小可知.
),c=f(2)=f(0)进而利用自变量的大小求得函数的大小,则a,b,c的大小可知.
解答:解:由条件f(x+1)=-f(x),可以得:
f(x+2)=f((x+1)+1)=-f(x+1)=f(x),所以f(x)是个周期函数.周期为2.
又因为f(x)是偶函数,所以图象在[0,1]上是减函数.
a=f(3)=f(1+2)=f(1),
b=f(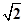 )=f(
)=f(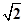 -2)=f(2-
-2)=f(2-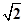 )
)
c=f(2)=f(0)
0<2-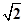 <1
<1
所以a<b<c
故选D
点评:本题主要考查了函数单调性,周期性和奇偶性的应用.考查了学生分析和推理的能力.

练习册系列答案
相关题目
已知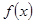 是R上的偶函数,且在区间
是R上的偶函数,且在区间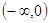 上是增函数,若
上是增函数,若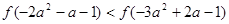 ,那么实数
,那么实数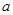 的取值范围是( )
的取值范围是( )
| A.(-1,0) | B.(-∞,0)∪(3,+∞) | C.(3,+∞) | D.(0,3) |
设函数 为奇函数,
为奇函数,
 = ( )
= ( )
| A.0 | B.1 | C. | D.5 |
给出下列三个函数图像:

它们对应的函数表达式分别满足下列性质中的至少一条:
①对任意实数
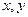 都有
都有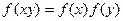 成立; ②对任意实数
成立; ②对任意实数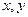 都有
都有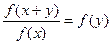 成立;
成立;③对任意实数
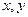 都有
都有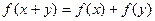 成立. 则下列对应关系最恰当的是
成立. 则下列对应关系最恰当的是 A. 和①, 和①,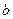 和②,c和③ 和②,c和③ | B.c和①,b和②, 和③ 和③ |
C.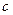 和①, 和①, 和②, 和②,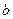 和③ 和③ | D.b和①,c和②, 和③ 和③ |
已知函数 的图像如图所示,则
的图像如图所示,则 的解析式可能是
的解析式可能是
A. | B. |
C. | D. |
若函数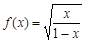 的定义域为A,函数
的定义域为A,函数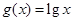 ,
,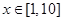 的值域为B,则A
的值域为B,则A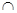 B为
B为
A.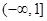 | B.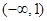 | C.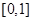 | D.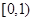 |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.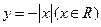 | B.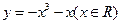 | C.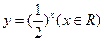 | D.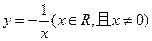 |
若x>0,  的最小值为( )
的最小值为( )
| A.12 | B.-12 | C.6 | D.-6 |
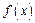 是定义在
是定义在 上的函数,且对于任意的
上的函数,且对于任意的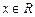 ,有
,有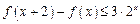 ,
,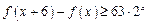 ,若
,若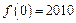 ,则
,则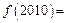 ( )
( ) .
.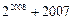
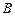 .
.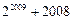
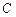 .
.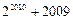
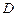 .
.