题目内容
设函数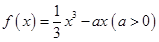 ,
,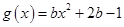 .
.
(1)若曲线 与
与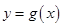 在它们的交点
在它们的交点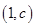 处有相同的切线,求实数
处有相同的切线,求实数 、
、 的值;
的值;
(2)当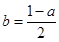 时,若函数
时,若函数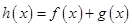 在区间
在区间 内恰有两个零点,求实数
内恰有两个零点,求实数 的取值范围;
的取值范围;
(3)当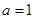 ,
,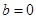 时,求函数
时,求函数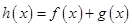 在区间
在区间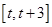 上的最小值.
上的最小值.
(1) ;(2)
;(2)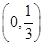 ;(3)
;(3) .
.
解析试题分析:(1)从条件“曲线 与
与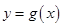 在它们的交点
在它们的交点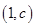 处有相同的切线”得到
处有相同的切线”得到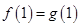 以及
以及 ,从而列有关
,从而列有关 、
、 的二元方程组,从而求出
的二元方程组,从而求出 与
与 的值;(2)将
的值;(2)将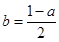 代入函数
代入函数 的解析式,利用导数分析函数
的解析式,利用导数分析函数 在区间
在区间 上的单调性,确定函数
上的单调性,确定函数 在区间
在区间 上是单峰函数后,然后对函数
上是单峰函数后,然后对函数 的端点值与峰值进行限制,列不等式组解出
的端点值与峰值进行限制,列不等式组解出 的取值范围;(3)将
的取值范围;(3)将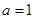 ,
,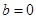 代入函数
代入函数 的解析式,并求出函数
的解析式,并求出函数 的单调区间,对函数
的单调区间,对函数 的极值点是否在区间
的极值点是否在区间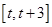 内进行分类讨论,结合函数的单调性确定函数
内进行分类讨论,结合函数的单调性确定函数 在区间
在区间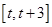 上的最小值.
上的最小值.
试题解析:(1)因为 ,
,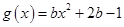 ,所以
,所以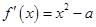 ,
,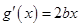 .
.
因为曲线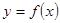 与
与 在它们的交点
在它们的交点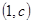 处有相同切线,
处有相同切线,
所以 ,且
,且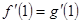 ,
,
即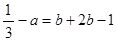 ,且
,且 ,解得
,解得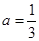 ,
, ;
;
(2)当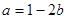 时,
时,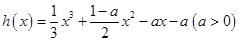 ,
,
所以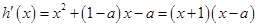 ,
,
令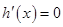 ,解得
,解得 ,
,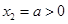 ,
,
当 变化时,
变化时, 、
、 的变化情况如下表:
的变化情况如下表:





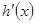
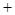

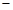

<
 练习册系列答案
练习册系列答案
西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
萌齐小升初强化模拟训练系列答案
相关题目
 (
(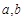 为常数),其图象是曲线
为常数),其图象是曲线 .
. 时,求函数
时,求函数 的单调减区间;
的单调减区间; ,若存在唯一的实数
,若存在唯一的实数 ,使得
,使得 与
与 同时成立,求实数
同时成立,求实数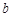 的取值范围;
的取值范围;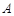 为曲线
为曲线 与曲线
与曲线 ,在点
,在点 ,设切线
,设切线 的斜率分别为
的斜率分别为 .问:是否存在常数
.问:是否存在常数 ,使得
,使得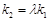 ?若存在,求出
?若存在,求出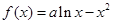 .
.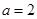 时,求函数
时,求函数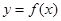 在
在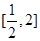 上的最大值;
上的最大值;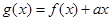 ,若
,若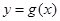 在区间
在区间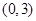 上不单调,求
上不单调,求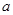 的取值范围;
的取值范围;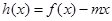 的图象与
的图象与 轴交于两点
轴交于两点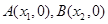 ,且
,且 ,又
,又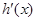 是
是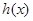 的导函数.若正常数
的导函数.若正常数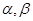 满足条件
满足条件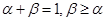 .证明:
.证明: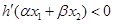 .
. 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用 亿元,至多
亿元,至多 亿元;③每年用于风景区改造费用
亿元;③每年用于风景区改造费用 ,
, ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=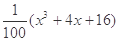 作为生态环境改造投资方案.
作为生态环境改造投资方案.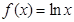 ,
,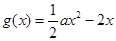 .
.
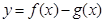 在
在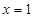 与
与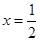 处的切线相互平行,求
处的切线相互平行,求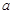 的值及切线斜率;
的值及切线斜率;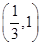 上单调递减,求
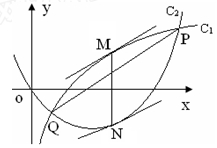
上单调递减,求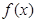 的图像C1与函数
的图像C1与函数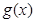 的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.
的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.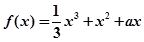 .
. 在区间
在区间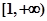 单调递增,求
单调递增,求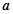 的最小值;
的最小值;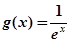 ,对
,对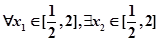 ,使
,使 成立,求
成立,求 的范围.
的范围. ,函数
,函数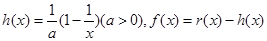 .
.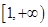 上是单调递增函数,试求实数a的取值范围:
上是单调递增函数,试求实数a的取值范围: 是公差为1.首项为l的等差数列,数列
是公差为1.首项为l的等差数列,数列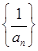 的前n项和为
的前n项和为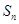 ,求证:当
,求证:当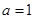 时,
时,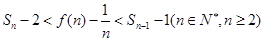 .
. ,
,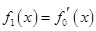 ,
,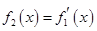 ,
,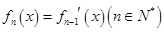 .
.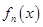 表达式(不需证明);
表达式(不需证明);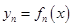 ;
;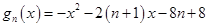 ,
, 的最大值为
的最大值为 ,
,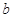 ,试求
,试求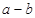 的最小值.
的最小值.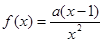 ,其中
,其中 .
. 的单调区间;
的单调区间;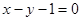 是曲线
是曲线 的切线,求实数
的切线,求实数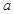 的值;
的值;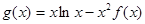 ,求
,求 在区间
在区间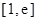 上的最小值.(
上的最小值.( 为自然对数的底数)
为自然对数的底数)