题目内容
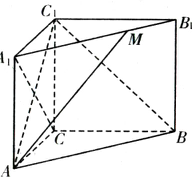 (2013•南京二模)如图,在直三棱柱ABC-A1B1C1中,CA=4,CB=4,CC1=2
(2013•南京二模)如图,在直三棱柱ABC-A1B1C1中,CA=4,CB=4,CC1=2| 2 |
(1)若A1M=3MB1,求异面直线AM与A1C所成角的余弦值;
(2)若直线AM与平面ABC1所成角为30°,试确定点M的位置.
分析:(1)以CA、CB、CC1为x、y、z轴,建立如图所示空间直角坐标系.算出向量
、
的坐标,利用空间向量的夹角公式,即可求出异面直线AM与A1C所成角的余弦值为
;
(2)利用垂直向量数量积为零的方程,建立方程组解出
=(1,1,
)是平面ABC1的一个法向量,设A1M=x,则
=(x-4,4-x,2
),结合题意可得
与
所成角为60°或120°,利用空间向量夹角公式建立关于x的方程解出x的值,即可得到点M为线段A1B1的中点时,满足直线AM与平面ABC1所成角为30°.
| CA1 |
| AM |
| ||
| 39 |
(2)利用垂直向量数量积为零的方程,建立方程组解出
| n |
| 2 |
| AM |
| 2 |
| AM |
| n |
解答:解:(1)分别以CA、CB、CC1为x、y、z轴,建立空间直角坐标系,如图所示
则C(0,0,0),A(4,0,0),A1(4,0,2
),B1(0,4,2
)
∵A1M=3MB1,∴M(1,3,2
),
可得
=(4,0,2
),
=(-3,3,2
),
∴cos<
,
>=
=
=-
由于异面直线所成角为直角或锐角,所以异面直线AM与A1C所成角的余弦值为
;
(2)由(1)得B(0,4,0),B1(0,0,2
)
∴
=(-4,4,0),
=(-4,0,2
)
设
=(a,b,c)是平面ABC1的一个法向量,可得
,取a=1,得b=1,c=
∴
=(1,1,
),而直线AM与平面ABC1所成角为30°,
可得
与
所成角为60°或120°
∴|cos<
、
>|=
,设A1M=x,则
=(x-4,4-x,2
)
即
=
=
=
解之得x=2或6,由于M在A1B1上可得x<6,故A1M=x=2
即点M为线段A1B1的中点时,满足直线AM与平面ABC1所成角为30°.
则C(0,0,0),A(4,0,0),A1(4,0,2
| 2 |
| 2 |
∵A1M=3MB1,∴M(1,3,2
| 2 |
可得
| CA1 |
| 2 |
| AM |
| 2 |
∴cos<
| CA1 |
| AM |
| ||||
|
| -4 | ||||
|
| ||
| 39 |
由于异面直线所成角为直角或锐角,所以异面直线AM与A1C所成角的余弦值为
| ||
| 39 |
(2)由(1)得B(0,4,0),B1(0,0,2
| 2 |

∴
| AB |
| AC1 |
| 2 |
设
| n |
|
| 2 |
∴
| n |
| 2 |
可得
| AM |
| n |
∴|cos<
| AM |
| n |
| 1 |
| 2 |
| AM |
| 2 |
即
| ||||
|
1•(x-4)+1•(4-x)+
| ||||
2
|
=
| 2 | ||
|
| 1 |
| 2 |
解之得x=2或6,由于M在A1B1上可得x<6,故A1M=x=2
即点M为线段A1B1的中点时,满足直线AM与平面ABC1所成角为30°.
点评:本题建立空间坐标系,求异面直线所成角和直线与平面所成角.着重考查了空间向量的夹角公式、平面法向量的求法和利用空间坐标系研究空间角等知识点,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
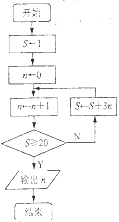 (2013•南京二模)如图是一个算法流程图,其输出的n的值是
(2013•南京二模)如图是一个算法流程图,其输出的n的值是