题目内容

若a、b、c∈R+,求证:≥abc.?

思路分析:不等式的形式对称,可考虑综合法证明.?

证明:?

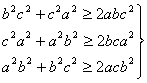
a2b2+b2c2+c2a2≥abc(a+b+c).?

∵a、b、c∈R+,∴a+b+c＞0.?

∴≥abc.?

思维陷阱:本题易犯如下的错误:?

由a、b、c∈R+,得b2c2+c2a2+a2b2≥3＞0,??

a+b+c≥3.?

两式相除得≥abc.

练习册系列答案
相关题目
28、（1）一次函数f（x）=kx+h（k≠0），若m＜n有f（m）＞0，f（n）＞0，则对于任意x∈（m，n）都有f（x）＞0，试证明之；
（2）试用上面结论证明下面的命题：若a，b，c∈R且|a|＜1，|b|＜1，|c|＜1，则ab+bc+ca＞-1．
若a，b，c∈R+，且a+b+c=1，求
a
+
b
+
c
的最大值．
若a＞b且c∈R，则下列不等式中一定成立的是（　　）
若a、b、c∈R，且|a-c|＜|b|，则（　　）
对于函数f（x），若?a，b，c∈R，f（a），f（b），f（c）为某一三角形的三边长，则称f（x）为“可构造三角形函数”．已知函数f（x）=
ex+t
ex+1
是“可构造三角形函数”，则实数t的取值范围是（　　）
A、[
1
2
，2]
B、[0，1]
C、[1，2]
D、[0，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网