题目内容
设 分别为两个不同的平面,直线
分别为两个不同的平面,直线 ,则“
,则“ ”是“
”是“ ”成立的( )
”成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
A
解析试题分析:根据两个平面垂直的判定定理知“ ”是“
”是“ ”的充分条件,但由两个平面垂直的性质知
”的充分条件,但由两个平面垂直的性质知 时,平面
时,平面 只有内只有和它们的交线垂直的直线才能垂直于平面
只有内只有和它们的交线垂直的直线才能垂直于平面 ,故本题中由“
,故本题中由“ ”不能得到“
”不能得到“ ”,因此选A.
”,因此选A.
考点:两个平面垂直的判定与性质.

练习册系列答案
相关题目
p:|x|>2是q:x<﹣2的( )条件
| A.充分必要 | B.充分不必要 |
| C.必要不充分 | D.既不充分也不必要 |
设 ,则
,则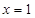 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知 、
、 为非零向量,则“
为非零向量,则“

 ”是“函数
”是“函数 为一次函数”的( )
为一次函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列四个命题中的真命题为( )
A. ,使得 ,使得 | B. ,总有 ,总有 |
C.  , ,  , , | D. , ,  , , |
若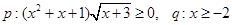 ,则p是q的 ( )
,则p是q的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题 :对任意
:对任意 ,
, 的否定是( )
的否定是( )
A. :对任意 :对任意 , , |
B. :不存在 :不存在 , , |
C. :存在 :存在 , , |
D. :存在 :存在 , , |
“函数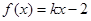 在区间
在区间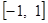 上存在零点”是“
上存在零点”是“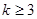 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |