题目内容
设 =4,若
=4,若 在
在 方向上的投影为2,且
方向上的投影为2,且 方向上的投影为1,则
方向上的投影为1,则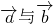 的夹角等于
的夹角等于
- A.

- B.

- C.

- D.

B
分析:利用向量的数量积的几何意义:向量的数量积等于一个向量的模乘以另一个向量在第一个向量上的投影;列出两个方程求出两个向量的模,再利用向量的数量积公式求出两个向量的夹角.
解答:设两个向量的夹角为θ,据题意
 即
即
所以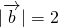
又 即
即
所以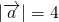
∵
∴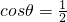
∴
故选B
点评:本题考查向量的数量积的几何意义;利用向量数量积的公式求出向量的夹角余弦.
分析:利用向量的数量积的几何意义:向量的数量积等于一个向量的模乘以另一个向量在第一个向量上的投影;列出两个方程求出两个向量的模,再利用向量的数量积公式求出两个向量的夹角.
解答:设两个向量的夹角为θ,据题意
 即
即
所以
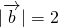
又
 即
即
所以
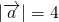
∵

∴
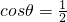
∴

故选B
点评:本题考查向量的数量积的几何意义;利用向量数量积的公式求出向量的夹角余弦.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =4,若
=4,若 在
在 方向上的投影为2,且
方向上的投影为2,且 方向上的投影为1,则
方向上的投影为1,则 的夹角等于( )
的夹角等于( )



 =4,若
=4,若 在
在 方向上的投影为2,且
方向上的投影为2,且 方向上的投影为1,则
方向上的投影为1,则 的夹角等于( )
的夹角等于( )



 =4,若
=4,若 在
在 方向上的投影为2,且
方向上的投影为2,且 方向上的投影为1,则
方向上的投影为1,则 的夹角等于( )
的夹角等于( )



 =4,若
=4,若 在
在 方向上的投影为2,且
方向上的投影为2,且 方向上的投影为1,则
方向上的投影为1,则 的夹角等于( )
的夹角等于( )



 =4,若
=4,若 在
在 方向上的投影为2,且
方向上的投影为2,且 方向上的投影为1,则
方向上的投影为1,则 的夹角等于( )
的夹角等于( )


