题目内容
1.设x>1,则函数g(x)=x+$\frac{9x}{x-1}$的最小值是16.分析 由题意可得t=x-1>0,可得x=t+1,换元可得y=10+t+$\frac{9}{t}$,由基本不等式可得.
解答 解:∵x>1,∴t=x-1>0,解得x=t+1,
∴换元可得y=t+1+$\frac{9(t+1)}{t}$=t+1+9+$\frac{9}{t}$
=10+t+$\frac{9}{t}$≥10+2$\sqrt{t•\frac{9}{t}}$=16,
当且仅当t=$\frac{9}{t}$即t=3即x=4时取等号.
故答案为:16.
点评 本题考查基本不等式求最值,换元是解决问题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.定义在R上的函数y=f(x),满足f(x+2)=-$\frac{1}{f(x)}$,则( )
| A. | f(x)不是周期函数 | B. | f(x)是周期函数,且最小正周期为2 | ||
| C. | f(x)是周期函数,且最小正周期为4 | D. | f(x)是周期函数,且4是它的一个周期 |
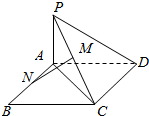 如图:ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=2,M、N分别是PC、AB中点,请选择适当的坐标系证明:MN⊥平面PCD.
如图:ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=2,M、N分别是PC、AB中点,请选择适当的坐标系证明:MN⊥平面PCD.