题目内容
已知数列{an}满足
(1)求证:数列{an}的奇数项,偶数项均构成等差数列;
(2)求{an}的通项公式;
(3)设
 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
【答案】分析:(1)由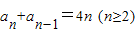 ①,得
①,得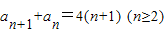 ②,两式相减得一递推式,根据等差数列的定义可得结论;
②,两式相减得一递推式,根据等差数列的定义可得结论;
(2)由a1=3,易求a2=5,根据等差数列可得a2n-1,a2n,通过变形整理可得an;
(3)利用错位相减法即可求得Sn.
解答:(1)由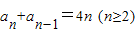 ①,
①,
得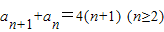 ②,
②,
②-①得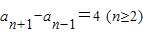 ,
,
所以数列{an}的奇数项,偶数项均构成等差数列,且公差都为4.
(2)由a1=3,a2+a1=8得a2=5,
故a2n-1=3+4(n-1)=4n-1,a2n=5+4(n-1)=4n+1,
由于a2n-1=4n-1=2(2n-1)+1,a2n=4n+1=2(2n)+1,所以an=2n+1;
(3)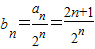 ,
,
所以Sn=b1+b2+…+bn=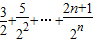 ①,
①,
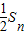 =
=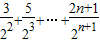 ②,
②,
①-②得,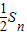 =
=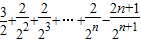 =
=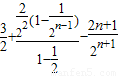 =
=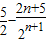 ,
,
所以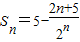 ;
;
点评:本题考查由数列递推式求数列通项公式、利用错位相减法对数列求和,考查学生解决问题的能力.
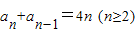 ①,得
①,得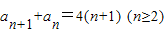 ②,两式相减得一递推式,根据等差数列的定义可得结论;
②,两式相减得一递推式,根据等差数列的定义可得结论;(2)由a1=3,易求a2=5,根据等差数列可得a2n-1,a2n,通过变形整理可得an;
(3)利用错位相减法即可求得Sn.
解答:(1)由
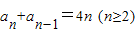 ①,
①,得
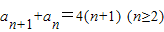 ②,
②,②-①得
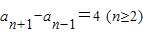 ,
,所以数列{an}的奇数项,偶数项均构成等差数列,且公差都为4.
(2)由a1=3,a2+a1=8得a2=5,
故a2n-1=3+4(n-1)=4n-1,a2n=5+4(n-1)=4n+1,
由于a2n-1=4n-1=2(2n-1)+1,a2n=4n+1=2(2n)+1,所以an=2n+1;
(3)
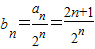 ,
,所以Sn=b1+b2+…+bn=
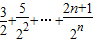 ①,
①,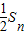 =
=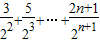 ②,
②,①-②得,
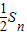 =
=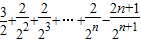 =
=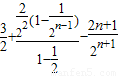 =
=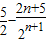 ,
,所以
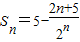 ;
;点评:本题考查由数列递推式求数列通项公式、利用错位相减法对数列求和,考查学生解决问题的能力.

练习册系列答案
相关题目