题目内容
已知方程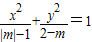
表示焦点在y轴上的椭圆，则m的取值范围是 ．
【答案】分析：方程表示焦点在y轴上的椭圆，所以y2的分母要大于x2的分母，并且这两个分母都是正数，由此建立关于m的不等式，解之即得m的取值范围．
解答：解：∵方程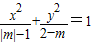
表示焦点在y轴上的椭圆，
∴2-m＞|m|-1＞0，解之得：1＜m＜
或m＜-1
故答案为：{m|1＜m＜
或m＜-1}
点评：本题给出含有字母参数的椭圆方程，在已知焦点位置的情况下求参数的取值范围，着重考查了椭圆的标准方程和基本概念，属于基础题．
解答：解：∵方程
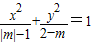表示焦点在y轴上的椭圆，∴2-m＞|m|-1＞0，解之得：1＜m＜
或m＜-1故答案为：{m|1＜m＜
或m＜-1}点评：本题给出含有字母参数的椭圆方程，在已知焦点位置的情况下求参数的取值范围，着重考查了椭圆的标准方程和基本概念，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
表示焦点在y轴上的双曲线，则k的取值范围是（ ）
表示焦点在y轴上的椭圆，则k的取值范围是（ ）
表示焦点在y轴上的椭圆，则实数k的取值范围是
B．
C．
D．
表示焦点在y轴上的椭圆，则实数k的取值范围是（
）
B．
C．
D．
表示焦点在y轴上的椭圆，则实数k的取值范围是（ ）
B．
C．
D．