题目内容
已知两个向量
 ,
, ,x∈[0,π].
,x∈[0,π].(1)求f(x)的值域;
(2)若
 ,求
,求 的值.
的值.
【答案】分析:(1)利用向量数量积的坐标运算,计算化简,将f(x)化为一角一函数形式,再求值域.
(2)若 ,得出
,得出 ,且判断出x为钝角,将x+
,且判断出x为钝角,将x+ 化成(x+
化成(x+ )+
)+ ,再利用两角和的余弦公式计算求解.
,再利用两角和的余弦公式计算求解.
解答:解:(1)由已知得 =cosx(2
=cosx(2 +sinx)+sinx(
+sinx)+sinx( -cosx)=
-cosx)=
∵x∈[0,π],∴
(2)由 又
又 ,
,
若x为锐角,则 ,矛盾,舍去
,矛盾,舍去
所以x为钝角,∴ ,
,
点评:本题考查三角函数公式的应用,三角函数的性质,向量的坐标运算.在(2)将x+ 化成(x+
化成(x+ )+
)+ ,再利用两角和的余弦公式计算 是关键.
,再利用两角和的余弦公式计算 是关键.
(2)若
 ,得出
,得出 ,且判断出x为钝角,将x+
,且判断出x为钝角,将x+ 化成(x+
化成(x+ )+
)+ ,再利用两角和的余弦公式计算求解.
,再利用两角和的余弦公式计算求解.解答:解:(1)由已知得
 =cosx(2
=cosx(2 +sinx)+sinx(
+sinx)+sinx( -cosx)=
-cosx)=
∵x∈[0,π],∴

(2)由
 又
又 ,
,若x为锐角,则
 ,矛盾,舍去
,矛盾,舍去所以x为钝角,∴
 ,
,
点评:本题考查三角函数公式的应用,三角函数的性质,向量的坐标运算.在(2)将x+
 化成(x+
化成(x+ )+
)+ ,再利用两角和的余弦公式计算 是关键.
,再利用两角和的余弦公式计算 是关键. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 ,
, ,x∈[0,π].
,x∈[0,π]. ,求
,求 的值.
的值. ,
,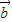 =(x,1).若(
=(x,1).若(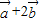 )∥(2
)∥(2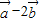 ),则x的值为 .
),则x的值为 .