题目内容
设函数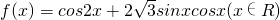 的最大值为M,若有10个互不相等的正数xi满足f(xi)=M,且xi<10π(i=1,2,…,10),则x1+x2+…+x10=________.
的最大值为M,若有10个互不相等的正数xi满足f(xi)=M,且xi<10π(i=1,2,…,10),则x1+x2+…+x10=________.

分析:由
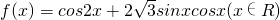 =2sin(2x+
=2sin(2x+ ),知f(x)周期为T=π,f(xi)=M为最大值,由2xi+
),知f(x)周期为T=π,f(xi)=M为最大值,由2xi+ =2kπ+
=2kπ+ ,xi=kπ+
,xi=kπ+ ,且xi<10π,知x1=
,且xi<10π,知x1= ,x2=
,x2= ,x3=2
,x3=2 ,…,x10=9
,…,x10=9 ,由此能求出x1+x2+…+x10.
,由此能求出x1+x2+…+x10.解答:∵
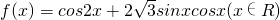
=cos2x+
 sin2x
sin2x=2sin(2x+
 ),
),∴f(x)周期为T=π,f(xi)=M为最大值,
∵2xi+
 =2kπ+
=2kπ+ ,xi=kπ+
,xi=kπ+ ,且xi<10π,
,且xi<10π,所以x1=
 ,x2=
,x2= ,x3=2
,x3=2 ,…,x10=9
,…,x10=9 ,
,∴x1+x2+…+x10=(0+1+2+3+…+9)π+10
 =
= .
.故答案为:
 .
.点评:本题考查正弦函数的定义域和值域的求法,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 的最大值为M,最小正周期为T.
的最大值为M,最小正周期为T. 满足
满足 求
求 的值.
的值. 的最大值为M,最小正周期为T.
的最大值为M,最小正周期为T. 的最大值为M,最小值为N,那么M+N=_____
的最大值为M,最小值为N,那么M+N=_____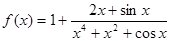 的最大值为M,最小值为m,则M+m的值为( )
的最大值为M,最小值为m,则M+m的值为( )