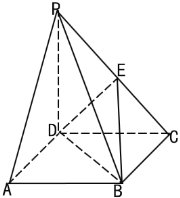
题目内容
【题目】如图,在棱长为1的正方体![]() 中,动点
中,动点![]() 在线段
在线段![]() 上运动,且有
上运动,且有![]() .
.

(1)若![]() ,求证:
,求证:![]() ;
;
(2)若二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)见证明;(2) ![]()
【解析】
(1)当![]() 时,
时,![]() 与
与![]() 重合,连接
重合,连接![]() ,可得
,可得![]() ,再由正方体特征可证得
,再由正方体特征可证得![]() ,即可证得
,即可证得![]() 平面
平面![]() ,问题得证。
,问题得证。
(2)以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系.分别求出平面
轴建立空间直角坐标系.分别求出平面![]() 的一个法向量
的一个法向量![]() 及平面
及平面![]() 的一个法向量
的一个法向量![]() ,利用向量夹角的坐标表示列方程即可求得
,利用向量夹角的坐标表示列方程即可求得![]() ,问题得解。
,问题得解。
(1)当![]() 时,
时,![]() 与
与![]() 重合,连接
重合,连接![]() ,
,
则在正方形![]() 中,
中,![]() .
.
又在正方体中![]() 底面
底面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() .
.
![]() ,所以
,所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() ,也即
,也即![]() .
.
(2)依题意,以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
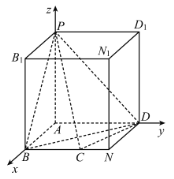
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则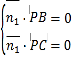 ,即
,即![]() ,
,
取![]() 得
得![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则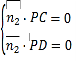 ,即
,即![]() ,
,
取![]() 得
得![]() .
.
所以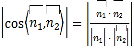
![]() ,
,
解得![]() 或
或![]() .
.
因为![]() ,所以
,所以![]() .
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
【题目】某单位共有职工1000人,其中男性700人,女性300人,为调查该单位职工每周平均体育运动时间的情况,采用分层抽样的方法,收集200位职工每周平均体育运动时间的样本数据(单位:小时).

(1)根据这200个样本数据,得到职工每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .估计该单位职工每周平均体育运动时间超过4小时的概率;
.估计该单位职工每周平均体育运动时间超过4小时的概率;
(2)估计该单位职工每周平均体育运动时间的平均数和中位数(保留两位小数);
(3)在样本数据中,有40位女职工的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有90%的把握认为“该单位职工的每周平均体育运动时间与性别有关”,
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附:![]() .
.