Question

直三棱柱ABC―A₁B₁C_l中，已知AB=BC=2，∠ABC=90°，异面直线A_lB与AC成60°角，点O、E分别为AC、BB_l的中点．

(Ⅰ)求证：OE∥平面AB₁C_l；

(Ⅱ)求证：A₁E⊥OC₁；

(Ⅲ)求二面角B₁一A₁C-C_l的大小．

Answer 1

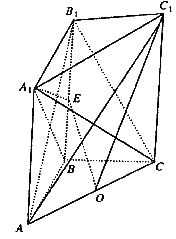
解：(Ⅰ)证明：取C_lC的中点F．连结EF、OF，则

  OF//AC₁，EF//B_l C₁

  ∴OF∥面AB_lC₁  EF∥面AB_lC₁．

  ∵EFOF=F,AC_l BC_l=C₁

  ∴平面OEF//平面AB₁C₁

  又∵OE平面OEF

  ∴OE∥平面AB_lC₁

  (Ⅱ)证明；取AB的中点G，连结B₁G，

  ∵A_l C₁∥AC

  又异面直线A₁B与AC成60°角，

  ∴∠BA_lC_l=60°

  在直三梭柱ABC-A₁B₁C₁中，AB=BC=2，

  ∠ABC=90°

  ∴A_lB=BC_1,A_lC_l=

  ∴AA₁=2

∴四边形ABA₁B₁ 为正方形

又E、G分别为BB₁、AB的中点

∴A_lE⊥B_lG

又B₁C₁⊥平面ABB₁A₁，

∴B₁C₁⊥A₁E

∵OG//BC，BC//B₁C₁

∴OG∥B₁C₁

∴O、G、B₁、C₁四点共面

∴A_lE⊥平面GB₁C₁   

∴A_lE⊥OC₁,

  (Ⅲ)取A₁C₁的中点H，则

  B₁H⊥A_lC₁

  ∴B_lH⊥平面CC_lA₁。

  过H作HM⊥A₁C，连结B_lM，则B_lM⊥A₁C，

  ∴∠B₁MH为二面角B₁―A₁C―C_l的平面角．

   在Rt△A_lC_lC和Rt△A_lMH中，A_lH=，C₁C=2，A_lC=

  ∴HM=

  又B_lH=

∴B₁MH=60°

  ∴二面角B_l-A_lC―C₁的大小为60°