题目内容
在研究函数
 的单调区间时,可用如下作法:设
的单调区间时,可用如下作法:设 得到
得到 在
在 ,
, 上是减函数,类比上述作法,研究
上是减函数,类比上述作法,研究
 的单调性,则其单调增区间为( )
的单调性,则其单调增区间为( )
A. | B. | C. | D. |
C
解析试题分析:设 ,因为
,因为 ,所以
,所以 单调递增,所以函数
单调递增,所以函数
 的单调增区间为
的单调增区间为 。
。
考点:类比推理;复合函数单调性的判断。
点评:此题主要考查的是类比推理。做此题的关键是设出函数 ,先得出函数
,先得出函数 的的单调区间,然后根据类比推理得出函数
的的单调区间,然后根据类比推理得出函数
 的单调增区间。此题有一定的难度。对学生的能力要求较高。
的单调增区间。此题有一定的难度。对学生的能力要求较高。

练习册系列答案
相关题目
若幂函数f(x)图像经过点P(4.2).则它在P点处的切线方程为( )
| A.8x-y-30=0 | B.x-4y+4=0 |
| C.8x+y-30=0 | D.x+4y+4=0 |
若 ,
, ,则
,则
A. | B. | C. | D. |
设函数 则
则 的值为 ( )
的值为 ( )
| A.a, b中较大的数 | B.a, b中较小的数 | C. a | D.b |
已知 函数
函数 的零点,若
的零点,若 ,则
,则 的值为( )
的值为( )
| A.恒为负值 | B.等于 | C.恒为正值 | D.不大于 |
设函数
 、
、 的零点分别为
的零点分别为 ,则( )
,则( )
A. | B. | C. | D. |
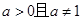 时,函数
时,函数 的图象只可能( )
的图象只可能( )
 是周期为2的奇函数,当0≤x≤1时,
是周期为2的奇函数,当0≤x≤1时, ,则
,则 ( )
( ) B -
B - C
C  )x的图象只可能是( )
)x的图象只可能是( )